Power Series |
|---|
DefinitionAny series which is of the form $\sum _{ n=0 }^{ \infty }{ { a }_{ n }{ (x-c) }^{ n } }$ is referred to Power Series. In many cases, we take $c$=0 to simplify the form (some times depending upon the function itself). Therefore we may also state that any series which is of the form is also a Power Series,
-1 |
MotivationFrom Taylor Series, we know how multiple derivatives of a function can be used to get a polynomial approximation of the same function. In Taylor series, we are adding up the terms which are different powers of $x$. i.e the obtained polynomial is an infinite series with a variable! Now in this polynomial form, for each power of $x$, we have an associated coefficient with it. We also know that for such an infinite series (which has a variable), there could only be certain values of $x$, for which the polynomial satisfies the function (or to be precise, have some converging value). Now is it possible to generalize the above case? Could we find the superset of the Taylor series? (as in Taylor series, the coefficients are fixed given the function!) We can indeed get such a generalized form by just generalizing the coefficients! i.e. 'Taylor Series' is associated with a particular function whereas a 'Power Series' might not be represented in a functional form (if it could not be represented in a particular function form, then it is referred to as a 'Taylor Series' instead of as a 'Power Series') Now, what can be said about their properties? What if we have two infinite series satisfying a few sets of properties and apply the algebraic operations over them? Would the resultant series even be satisfying all those properties? What exactly does infinite mean? Can we find the interval of $x$ for which the series converges, as computed in Taylor Series? (i.e. a generalized form for these intervals). If yes, would it show the same behavior for any set of coefficients? So we see how Power Series is a generalized form of Taylor Series which builds a route even to many other infinite series (having a variable).
Bird's eye viewFirst, let's look at the term "series". What does it mean? It simply refers to the "summation" of things (terms)! Now this summation could be finite or infinite. "Power Series" is simply an infinite series which is of the form: \[\sum _{ n=0 }^{ \infty }{ { a }_{ n }{ (x-c) }^{ n } }\] where ${ a }_{ n }$'s are constants or to be precise are coefficients of ${ (x-c) }^{ n }$ and $c$ is any constant and is sometimes referred to as "Centre of the Series". i.e. Power Series is simply adding up of infinite terms. Now for the given values of $c$ and $a_n$'s, it depends upon the value of $x$ whether the series can be approximated to a finite value or not (converges or diverges). Therefore for a given series, we might have the set of values of $x$ for which the series can converge. This range is called the Interval of convergence. And the radius of the circle (centered at $c$) we would be getting after considering the interval of convergence as the diameter, is referred to as Radius of convergence. (Refer Context for a detailed view) For the standard series, if $R$ is the radius of convergence, then one of the below four intervals would be the interval of convergence:
In general, the series itself could be represented as some function by considering the domain as the interval of convergence! 0 |
Context of the definitionHere the entire series itself can be represented with a function $f\left( x \right)$ which is a polynomial with infinite terms! Here we define the Domain of the function as, "The values of x for which the function,$f\left( x \right)$ converges" i.e. Here depending upon various values of ${ a }_{ i }$, we get different other series such as geometric series, Taylor series, etc. 0 |
|
0 |
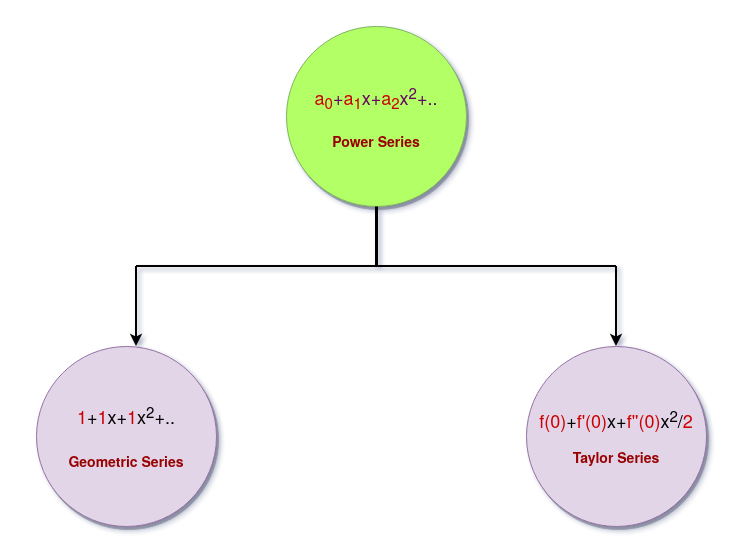
Figure 1 : Series connected to Power Series [Created using 'App.Diagrams'] |
|
Since we are dealing with infinite terms, the given series can either completely Converge or completely Diverge or can even Partially Converge in some interval of $x$. There are many methods to test for convergence such as integral tests, root tests, etc, and one of the famous ways could be to use Ratio Test. Here try using the most suitable test and there is no way to get which test could be used to get an answer! It's just a "Trail and error" method. So if any of the tests doesn't give a valid output, then go with other tests! 0 |
|
0 |
|
Video 1 : Convergence of Power Series |
|
There are certain other properties required for the above equation to satisfy. To be precise, the polynomial should satisfy the Cauchy convergence test for the sum of the terms to converge! (Try considering one of the classic examples, $a_{n}=\frac{1}{n}$) So we can generalise the 3 possibilites that exist for some series of form $\sum { { a }_{ n }{ (x }-c)^{ n } }$:
Here the term $R$ is known as Radius Of Convergence. Consider the power series of $\sum { (-1)^{ n }x^{ 2n } }$. Let us analyze to which of the above cases, it belongs to! 0 |
|
0 |
|
Video 2 : Example of a convergent series |
|
Radius Of Convergence Consider an infinite series $\sum { { a }_{ n }{ (x-c) }^{ n } }$,then the distance between $c$ and the max point,$x$ upto which the series converges is referred to as Radius Of Convergence. So in the above three conditions, $R$ in the first condition is $0$ and is $\infty$ in the second condition We basically have two ways to get it:
As we can decide on what values the series converges or diverges just by its radius of convergence, therefore a formal theorem has also been given for the same and is known as Cauchy-Hadamard Theorem. Cauchy-Hadamard Theorem : Consider the power series, $\sum { { a }_{ n }{ x }^{ n } }$. Let $R$ be the Radius Of Convergence, then the power series is absolutely convergent if $\left| x \right| <R$ and is absolutely divergent if $\left| x \right| >R$. 0 |
|
Interval Of Convergence It is simply the interval in which the series converges. Now for some series, $\sum { { a }_{ n }{ (x }-c)^{ n } }$ , let $R$ is the Radius Of Convergence, then we observe a circle centered at $c$ and having radius $R$. Hence the interval $(-R, R)$ is considered as Interval Of Convergence. Let us check out our old friend again, $\sum { (-1)^{ n }x^{ 2n } }$ . Let us try to find the radius of convergence and interval of convergence for this power series! 0 |
|
0 |
|
Video 3 : Radius And Interval of Convergence |
|
We always need to check if the series converges or diverges at the endpoints (i.e. at $c+R$ and $c-R$). Depending upon these, we modify the interval of convergence! 0 |
|
Theorems related to $R$ Theorem Let us analyze what exactly uniform convergence mean! We shall again take the help of our friend, $\sum { (-1)^{ n }x^{ 2n } }$. 0 |
|
0 |
|
Video 4 : Uniform Convergence of a Power Series |
|
The above animation is shown for a particular value of $x$. It can be shown in a similar way for all $x$ within the region of convergence for this particular $f(x)$. Theorem Uniqueness Theorem 0 |
|
Operations on Power Series If $f(x)=\sum { { a }_{ n }{ x }^{ n } }$ and $g(x)=\sum { { b }_{ n }{ x }^{ n } }$ then:
Therefore we can say that, if the power series can be depicted in the form of a function, then we can apply any algebraic operations on the series themselves and get the relevant results by applying the same operation on the function itself. Since the series themselves get into a new form, therefore their interval of convergence also changes accordingly! 0 |
Applications
0 |
HistoryPower Series is one of the oldest and the most important contribution to the field of mathematics, especially to the study of calculus. It was one of the earliest discoveries of Newton wherein he simply considered them as infinite decimal expansions of numbers. It even had been used much earlier by some of the mathematicians in certain cases. He started his study with the infinite geometric series and tried to apply the properties of power series to these series. He specifically considered the series $\frac {1}{1+x}$ which was, in fact, a very known and famous geometric series. Newton then proceeded his study over these series by considering the binomial power series $(1+x)^k$. This series is special in its way by making its general form of integral to depend upon the value of k (i.e. whether it is positive, negative, or a fraction!). He then considered the series of $(1+k)^{1/2}$ which we get by just taking k as 1/2. Now he observed that squaring its power series would result in (1+x) itself! This result resonated with his confidence and the path he is following. He then tried to differentiate and integrate the series term-by-term as these are simply polynomials (with infinite terms!) and compared with the expected results with the known methods. He proceeded with his study further and finally gave a huge contribution to the field of calculus! 1 |
References
Further Readings
1 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
