Linear Transformations (Linear Maps) |
|---|
DefinitionLet $V$ and $W$ be vector spaces over the field $F$. Linear Transformation from $V$ into $W$ is a function $T$ from $V$ into $W$ such that $\rightarrow$ $T(\alpha x+y)\ =\ \alpha\ T(x)\ +\ T(y)$ $\forall\ x$ and $y$ in $V$ and $\forall\ \alpha$ in $F$.
Note $\rightarrow$ We use the term "Linear Transformation" and "Linear Maps" interchangeably. 3 |
MotivationWe have been dealing with matrices from quiet some time now. But think if each and every matrix is linked with a linear transformation (which is a mapping of vectors from one vector space to another). These matrices or linear transformations are used for scaling, rotation, reflection, etc. There are many theorems and concepts which are built over linear transformation like four fundamental subspaces or rank-nullity theorem. They could be understood only after we understand linear transformation. 4 |
|
Say, you want to enlarge an image by a scale of 2 on your computer. You can use many tools for doing so. But how do these tools work? Well, these tools may be using linear transformations in the background, to achieve this purpose. Also if you want to rotate a figure, linear transformations can be used. For example, if you want to rotate the figure by 60$^{\circ}$, you may use Linear Transformation. So let us understand what linear transformations are. 5 |
Bird's Eye ViewLinear Transformation is a mapping of vectors of a vector space to another. Linear here implies that the linear transformation follows the linearity property. By linearity, we mean if you consider a grid(a group of straight lines), after linear transformation, all straight lines must either remain straight lines or sends to a point in the grid formed. Here, the origin must remain where it was before transformation (See video 1). Using Linear Transformation you can do the following transformations –
Note: There are other transformations also(which are primarily the combinations of Scaling, Rotation, and Shearing). 7 |
|
8 |
|
Video 1: Visually understanding linear transformation(using grid) |
Context Of DefinitionLet $V$ and $W$ be vector spaces over the field $F$. So we define a function $T$ from $V$ into $W$ such that $\rightarrow\ T(\alpha x+y)\ =\ \alpha\ T(x)\ +\ T(y)$ hold good for all $x$ and $y$ in $V$ and for all $\alpha$ in $F$. A function, say $T$, whose domain and range are vector spaces over field $F$, and satisfy these conditions $\rightarrow$
(OR) $\ T(\alpha x+y)\ =\ \alpha\ T(x)\ +\ T(y)$ then the function $T$ is a Linear Transformation from V into W. Transformation is just a synonym of a function and linearity is a property that preserves addition and scalar multiplication. i.e.
In Linear Transformations, the ratios of the distance between any 3 co-linear points after a linear transformation, must remain the same. A linear transformation is simply a linear mapping between two vector spaces. It is a function that takes in a vector $v\in V$($V$ is the domain of Linear Transformation) and returns a vector $T(v)\in W$($W$ is Co-Domain of Linear Transformation). You may also observe that it is indeed a mapping of every vector $v \in V$ to some vector $T(v)\in W$, so we use the term "Linear Transformation" and "Linear Maps" interchangeably. See video 2 for a basic understanding of linear transformations when form($i$) is given. 9 |
|
10 |
|
Video 2: Linear Transformation when form 1 is given |
Matrix Representation Of Linear TransformationLet us consider a Linear Transformation $T: R^2\rightarrow R^2$ defined by$\rightarrow$ $T(x,y) = (x+y,x-y)$ (Lets consider this as form 1) Claim$\rightarrow$ If $T:V \rightarrow W$ is linear transformation then $\exists$ matrix $A\ s.t.\ T$ can be written as $\rightarrow T(v)= A.v$ ...(Let us consider this as form 2) Considering the example above, you need to represent vectors involved in linear transformation as matrices: $T\left[\begin{array} {c} x \\ y \end{array}\right] = \left[\begin{array} {c} x+y \\ x-y \end{array}\right]$ $= \left[\begin{array} {c c} 1 & 1 \\ 1 & -1 \end{array}\right] \left[\begin{array} {c} x \\ y \end{array}\right]$ (Converting in form 2 by observation) Let us have a look at the derivation of the claim for $T:R^n \rightarrow R^m$ The $dim\ R^n=n$ and let $e_1,e_2,e_3, \cdots, e_n$ form the standard basis of $R$. Let x $\in R^n$ $\Rightarrow x= a_1 e_1 + a_2 e_2 + a_3 e_3 + \cdots + a_n e_n$ Representing $x$ as matrix multiplication of 2 matrices. $\Rightarrow x = \left[\begin{array} {c c c c c} e_1 & e_2 & e_3 & \cdots & e_n \end{array}\right] \left[\begin{array} {c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array}\right]$ As $e_1,e_2,e_3,\cdots,e_n$ forms the standard basis of $R^n \Rightarrow$ $\left[\begin{array} {c c c c c} e_1 & e_2 & e_3 & \cdots & e_n \end{array}\right]$ $\equiv$ $I_n$. $\Rightarrow x = I_n \left[\begin{array} {c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array}\right]$ $\Rightarrow x = \left[\begin{array} {c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array}\right]$ $\Rightarrow T(x) = T( a_1 e_1 + a_2 e_2 + a_3 e_3 + ... + a_n e_n)$ where $T$ is a Linear Transformation from $R^n$ into $R^m$. Using the Linear transformation properties - $\Rightarrow T(x) = T( a_1 e_1) + T(a_2 e_2) + T(a_3 e_3) + ... + T( a_n e_n)$ $\Rightarrow T(x) = a_1 T( e_1) + a_2 T( e_2) + a_3 T( e_3) + ... + a_n T( e_n)$ Representing $T(x)$ as matrix multiplication of 2 matrices. $\Rightarrow T(x) = \left[\begin{array} {c c c c c} T(e_1) & T(e_2) & T(e_3) & \cdots & T(e_n) \end{array}\right] \left[\begin{array} {c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array}\right]$ $\Rightarrow T(x) = Ax$ $where\ A = \left[\begin{array} {c c c c c} T(e_1) & T(e_2) & T(e_3) & \cdots & T(e_n) \end{array}\right]$
Refer to the video 3. 11 |
|
12 |
|
Video 3: Matrix Representation Of Linear Transformation |
Conversion of Form 1 to Form 2Consider the same example: $T(x,y) = (x+y,x-y)$ for vector space $R^2$ standard basis are $(1,0)$ and $(0,1)$ $T(1,0) = (1,1)$ $T(0,1) = (1,-1)$ As we know that $A = \left[\begin{array} {c c c c c} T(e_1) & T(e_2) & T(e_3) & \cdots & T(e_n) \end{array}\right]$ $\Rightarrow$ Here, $A = \left[\begin{array} {c c} 1 & 1\\ 1 & -1 \end{array}\right]$ 13 |
Common Linear TransformationsScaling, Rotation and ShearingThe standard basis of $R^2$ are $\hat{i}$ and $\hat{j}$, so a general vector $x \in R^2$ can be writen as $\rightarrow$ Let $T$ be a linear transformation function so equation $(i)$ can be written as, $\Rightarrow x_{transformed} = a*\hat{i}_{transformed} + b*\hat{j}_{transformed}$ Let us understand what Linear Transformations imply visually(See video 4). 14 |
|
15 |
|
video 4: Understand Linear Transformations visually |
|
Note: For representation purposes we sometimes represent a vector(usually represented by an arrow) as a point as there may be too many vectors to represented at the same time. ScalingScaling in context of linear transformation means to increase(enlarge) or decrease(diminish) by at least one scalar factor of a vector. There are 2 types of scaling -
Let us discuss this with respect to a linear transformation $T:R^2\rightarrow R^2$ 16 |
Uniform ScalingIf we want to scale a vector by scaling factor of $S$ then $\rightarrow$ T($\left[\begin{array} {c} 1 \\ 0 \end{array}\right]$) = $S \left[\begin{array} {c} 1 \\ 0 \end{array}\right]$ or $\left[\begin{array} {c} S \\ 0 \end{array}\right]$ T($\left[\begin{array} {c} 0 \\ 1 \end{array}\right]$) = $S \left[\begin{array} {c} 0 \\ 1 \end{array}\right]$ or $\left[\begin{array} {c} 0 \\ S \end{array}\right]$ $\Rightarrow T(\vec{v})$ = $\left[\begin{array} {c} T(\left[\begin{array} {c} 0 \\ 1 \end{array}\right]) & T(\left[\begin{array} {c} 0 \\ 1 \end{array}\right]) \end{array}\right] = \left[\begin{array} {c c} S & 0 \\ 0 & S \end{array}\right] \vec{v} = S \left[\begin{array} {c} 1 & 0 \\ 0 & 1 \end{array}\right] \vec{v} = S \vec{v}$ See video 5. 17 |
|
18 |
|
video 5: Uniform Scaling |
Non-Uniform ScalingIf we want to scale $\left[\begin{array} {c} 1 \\ 0 \end{array}\right]$ by a scaling factor of $S_{\hat{i}}$ and $\left[\begin{array} {c} 0 \\ 1 \end{array}\right]$ by a scaling factor of $S_{\hat{j}}$ then $\rightarrow$ T($\left[\begin{array} {c} 1 \\ 0 \end{array}\right]$) = $S_{\hat{i}} \left[\begin{array} {c} 1 \\ 0 \end{array}\right]$ or $\left[\begin{array} {c} S_{\hat{i}} \\ 0 \end{array}\right]$ T($\left[\begin{array} {c} 0 \\ 1 \end{array}\right]$) = $S_{\hat{j}} \left[\begin{array} {c} 0 \\ 1 \end{array}\right]$ or $\left[\begin{array} {c} 0 \\ S_{\hat{j}} \end{array}\right]$ $\Rightarrow T(\vec{v}) = \left[\begin{array} {c} T(\left[\begin{array} {c} 0 \\ 1 \end{array}\right]) & T(\left[\begin{array} {c} 0 \\ 1 \end{array}\right]) \end{array}\right] = \left[\begin{array} {c c} S_{\hat{i}} & 0 \\ 0 & S_{\hat{j}} \end{array}\right] \vec{v}$ 19 |
ShearingFor a linear tranformation $T:R^2\rightarrow R^2$, according to wolfram alpha shearing transformation is the one, in which, "all points along a given line remain fixed while other points are shifted parallel to line by a distance proportional to their perpendicular distance from line." [9]
In three dimensions, planes are translated instead of lines. Here, we will be discussing about 2 shearing transformation in $R^2$-
20 |
Horizontal ShearIn $R^2$, horizontal shear is a transformation in which all the points along x-axis remain fixed while other points are shifted parallel to x-axis by a distance proportional to their perpendicular distance from x-axis.(See Figure 1) 21 |
|
22 |
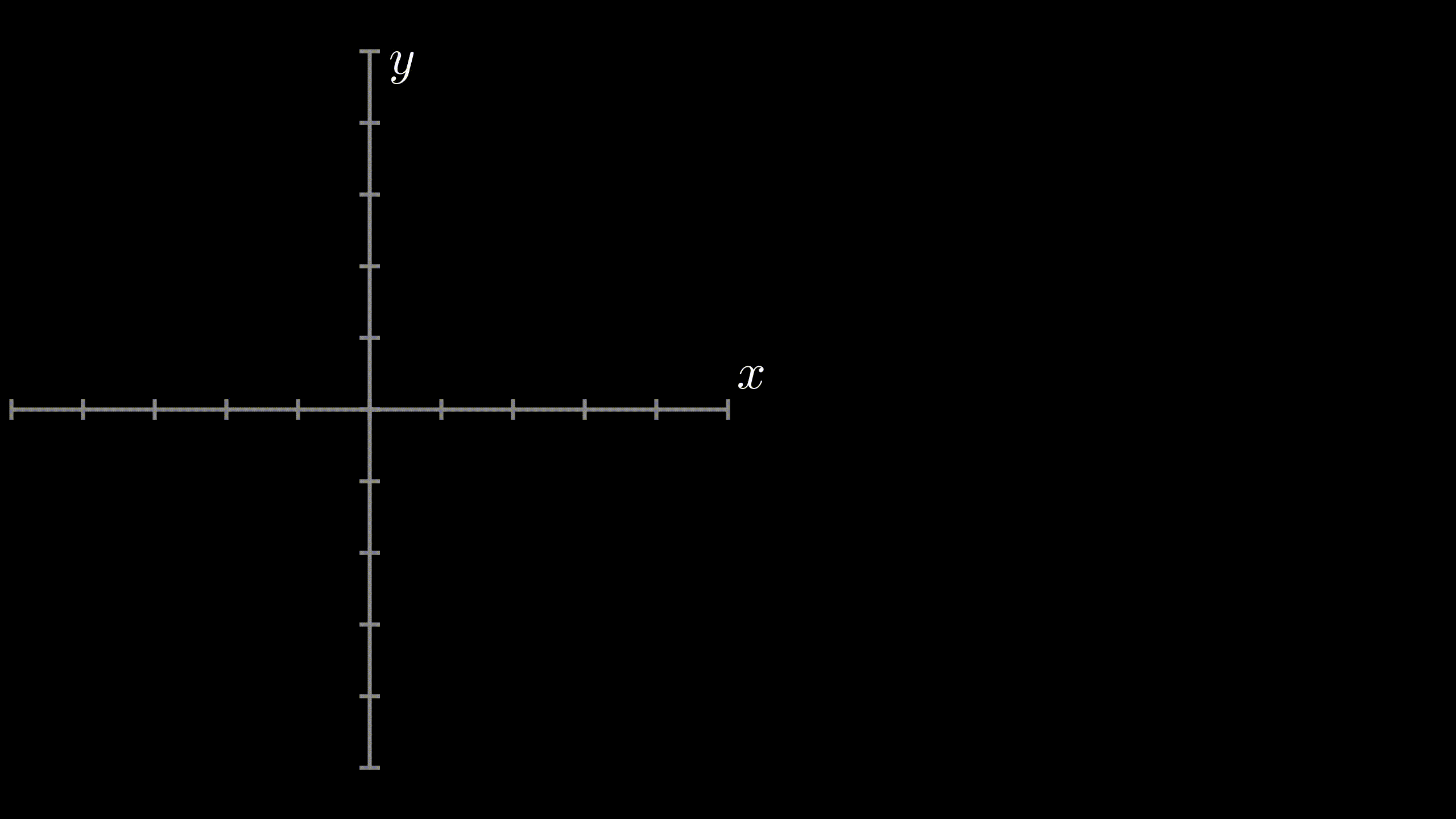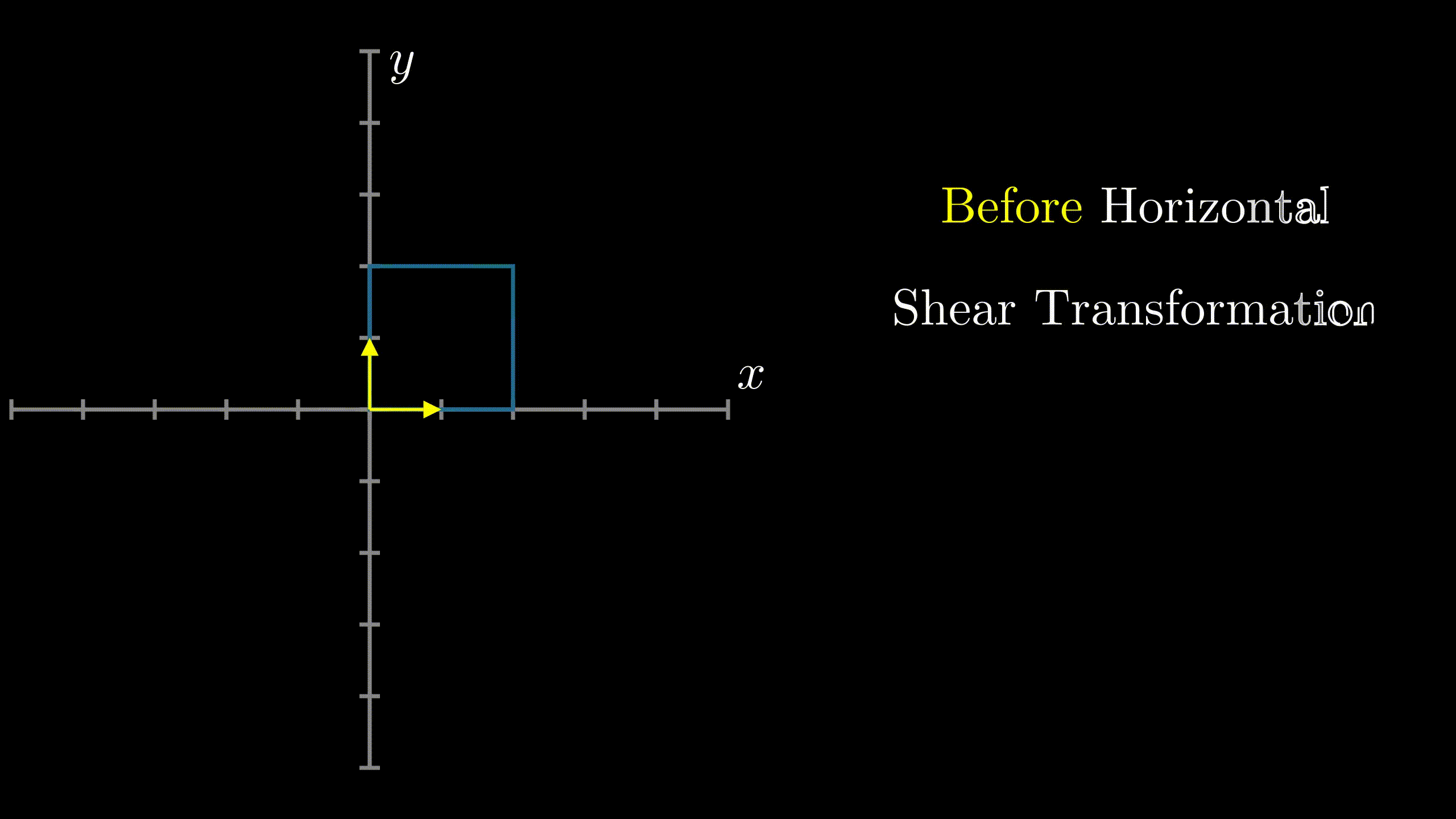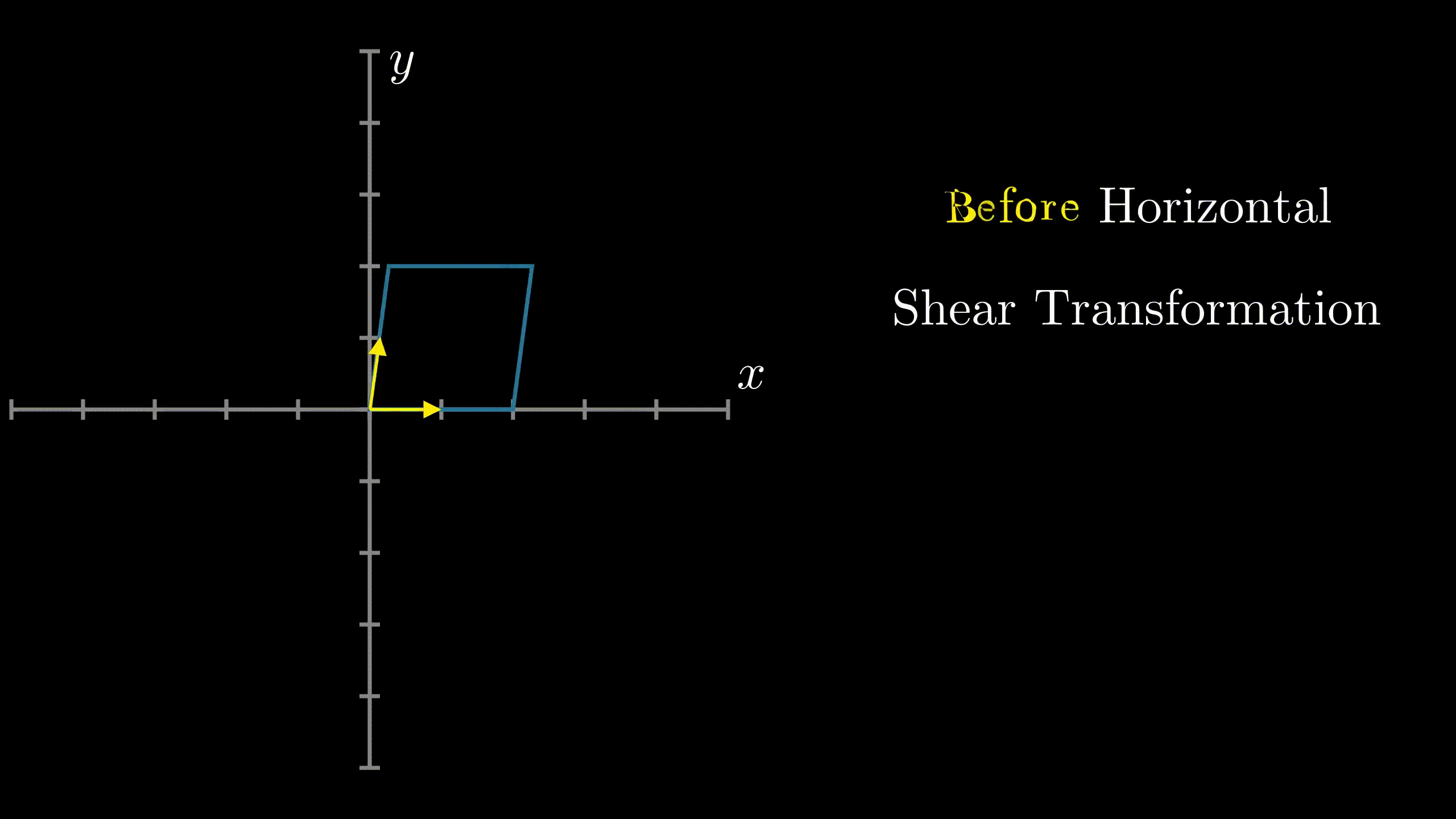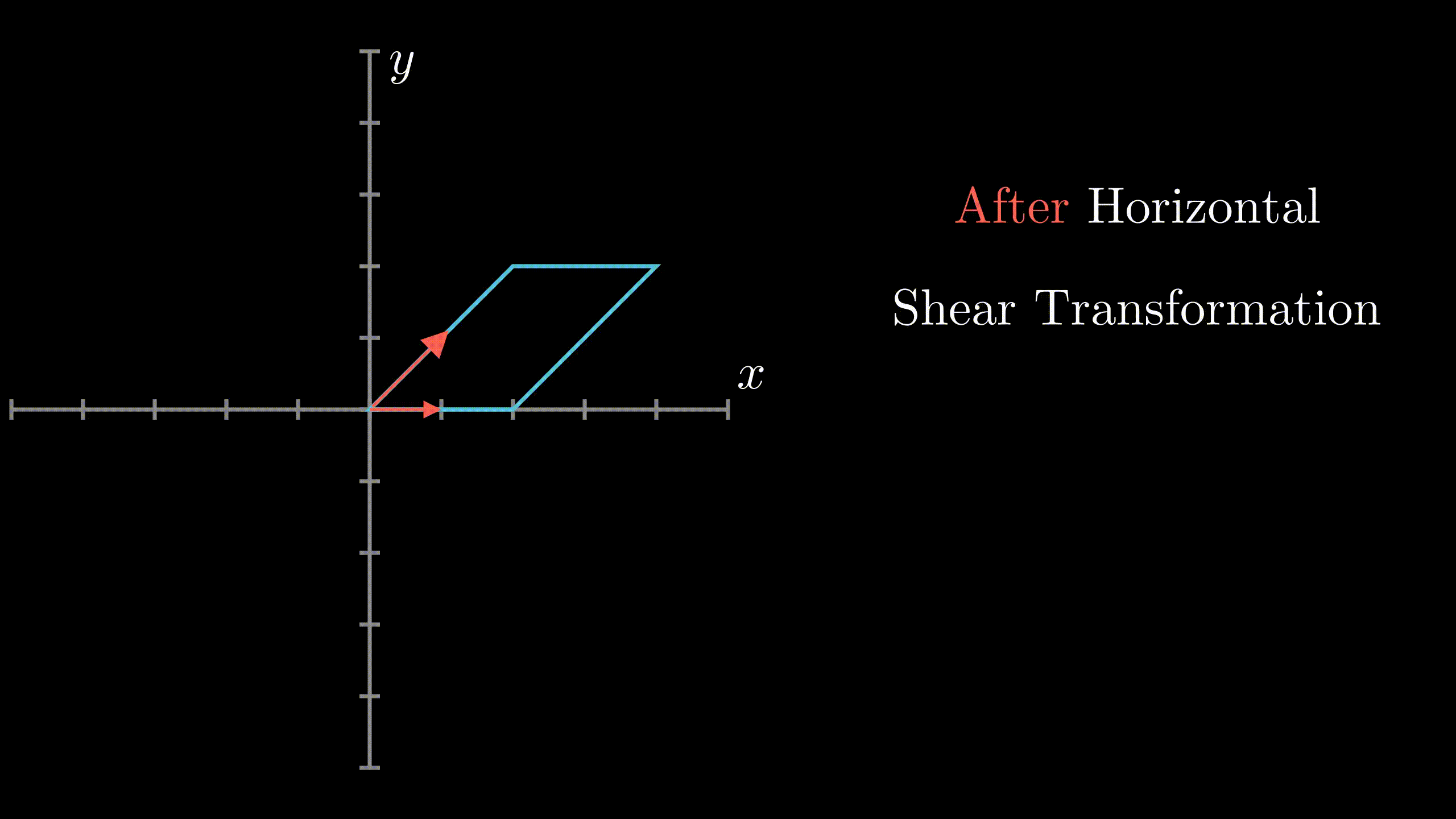
Fig.1 Horizontal Shear |
|
Observe the standard basis $\left[ \begin{array} {c}1\\ 0 \end{array}\right]$ and $\left[ \begin{array} {c}0 \\ 1 \end{array}\right]$.From Fig. 1, we can see $\rightarrow$ $T(\left[ \begin{array} {c}1\\ 0 \end{array}\right]) = \left[ \begin{array} {c}1\\ 0 \end{array}\right]$ $T(\left[ \begin{array} {c}0\\ 1 \end{array}\right]) = \left[ \begin{array} {c}1\\ 1 \end{array}\right]$ $\Rightarrow$ Matrix of linear transformation for horizontal shear = $\left[ \begin{array} {c c}1 & 1\\ 0 & 1 \end{array}\right]$ Note: General Matrix of linear transformation for horizontal shear is of form $\left[ \begin{array} {c c}1 & k_x\\ 0 & 1 \end{array}\right]$ 23 |
Vertical ShearIn $R^2$, vertical shear is a transformation in which all the points along y-axis remain fixed while other points are shifted parallel to y-axis by a distance proportional to their perpendicular distance from y-axis.(See Figure 2) 24 |
|
25 |
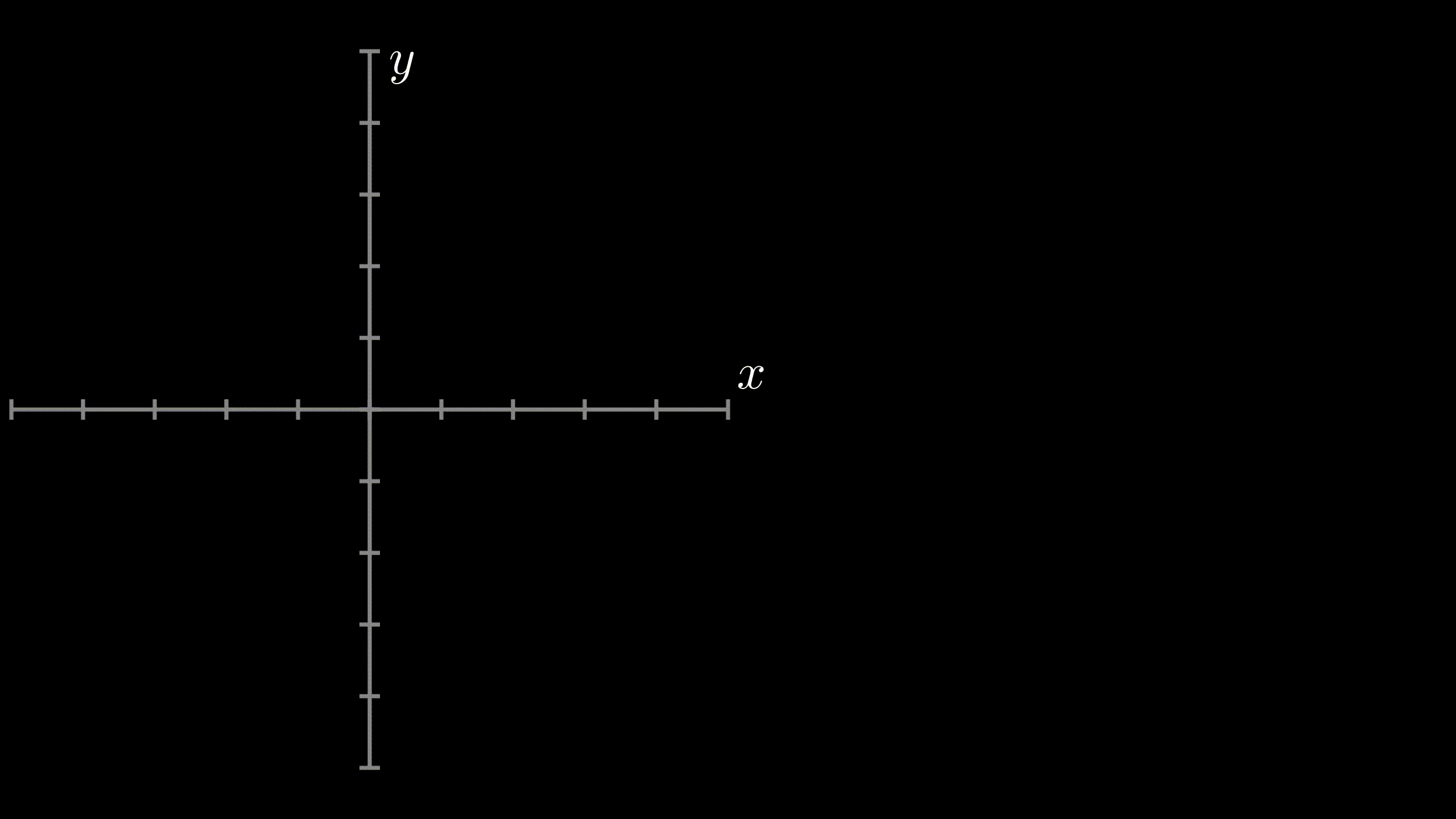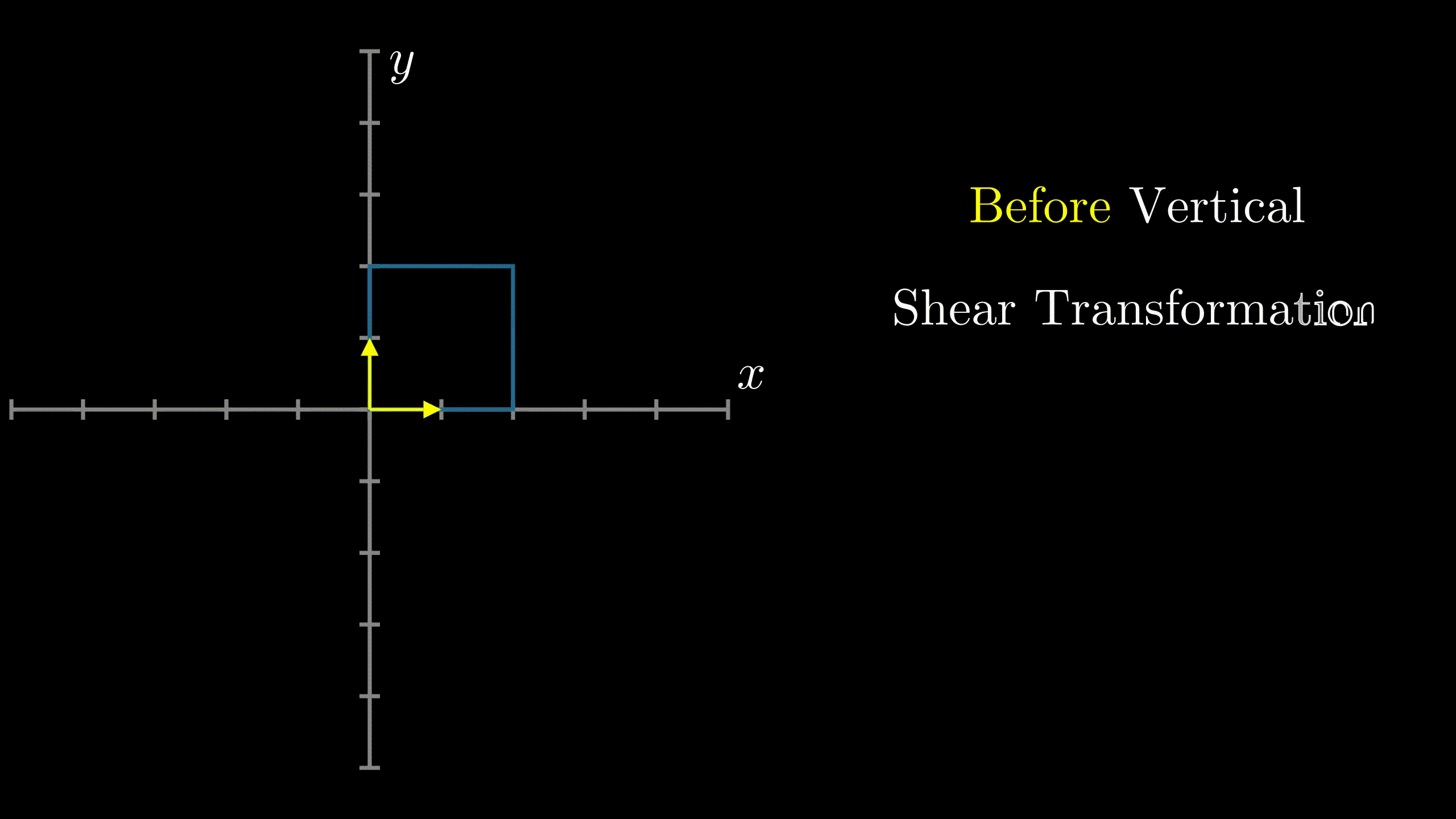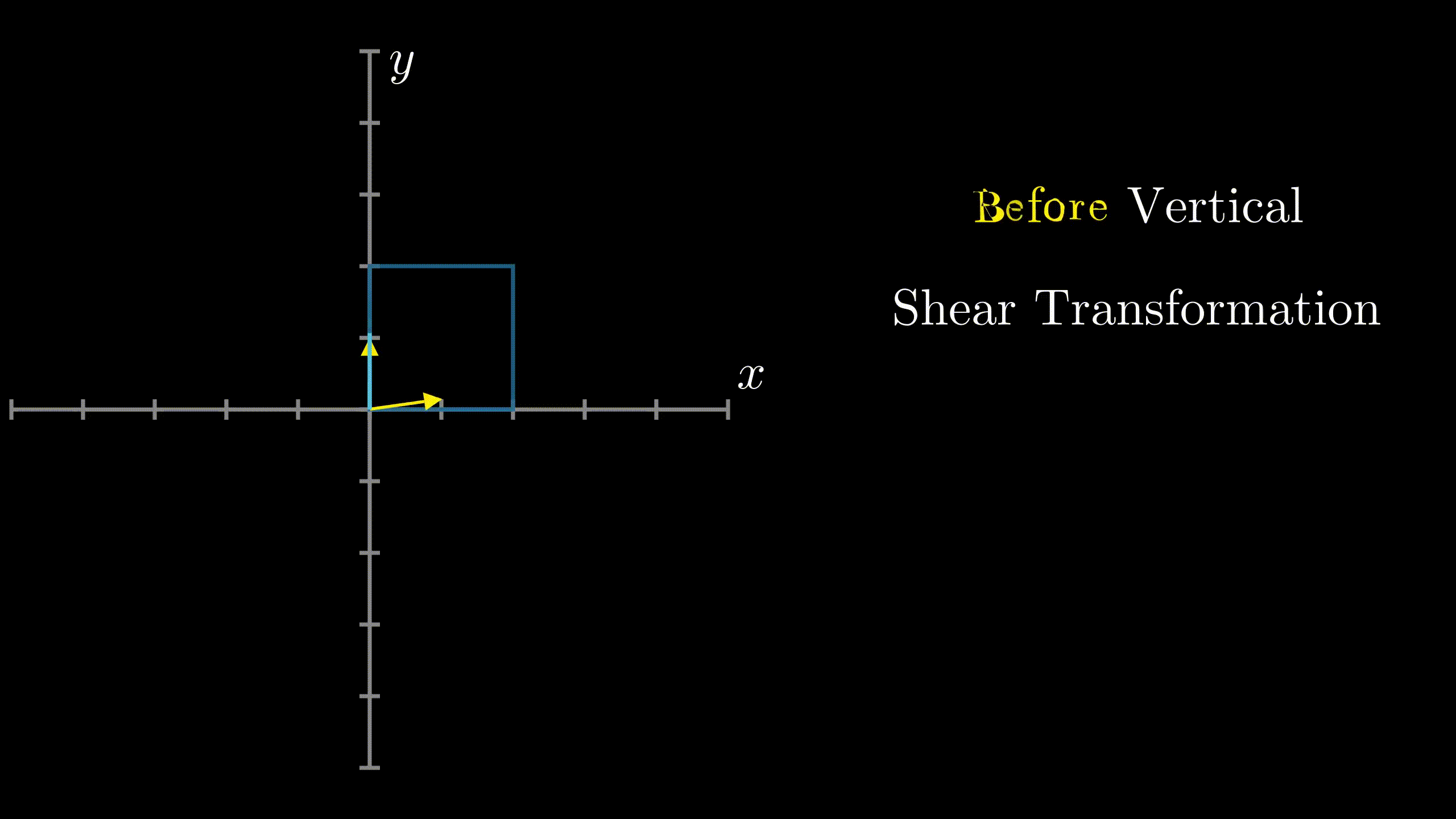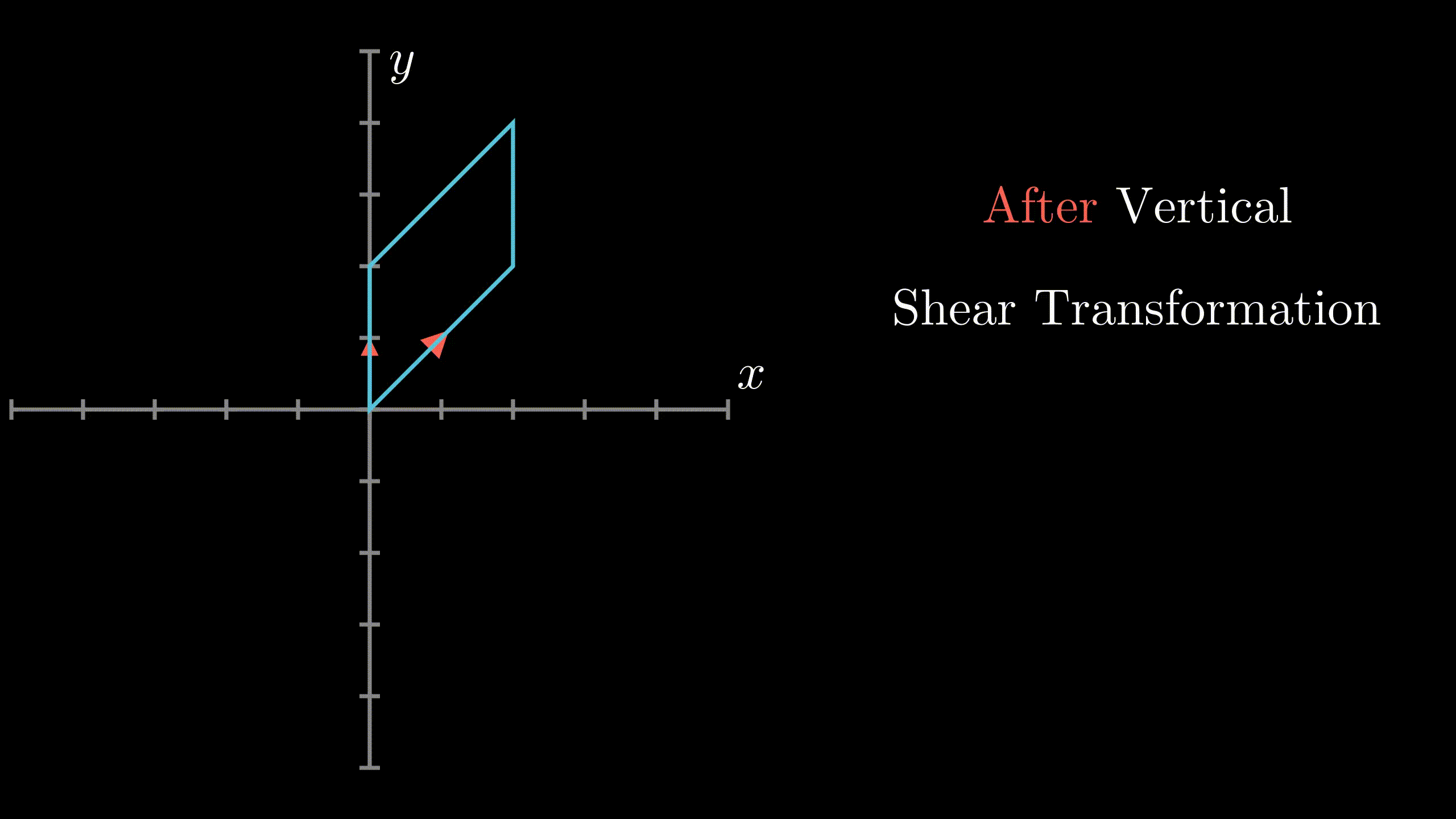
Fig.2 Vertical Shear |
|
Observe the standard basis $\left[ \begin{array} {c}1\\ 0 \end{array}\right]$ and $\left[ \begin{array} {c}0 \\ 1 \end{array}\right]$.From Fig. 2, we can see $\rightarrow$ $T(\left[ \begin{array} {c}1\\ 0 \end{array}\right]) = \left[ \begin{array} {c}1\\ 1 \end{array}\right]$ $T(\left[ \begin{array} {c}0\\ 1 \end{array}\right]) = \left[ \begin{array} {c} 0\\ 1 \end{array}\right]$ $\Rightarrow$ Matrix of linear transformation for vertical shear = $\left[ \begin{array} {c c}1 & 0\\ 1 & 1 \end{array}\right]$ Note: General Matrix of linear transformation for vertical shear is of form $\left[ \begin{array} {c c}1 & 0\\ k_y & 1 \end{array}\right]$ 26 |
RotationA simple example of how rotation can be achieved using Linear Transformation can be see in Video 1. So, now we will look at the matrix of linear transformation for rotation in $R^2$. 27 |
|
28 |
|
video 6: Rotation by an angle of in anticlockwise direction |
|
Observe the standard basis $\left[ \begin{array} {c}1\\ 0 \end{array}\right]$ and $\left[ \begin{array} {c}0 \\ 1 \end{array}\right]$.From video 6, we can see $\rightarrow$ $T(\left[ \begin{array} {c}1\\ 0 \end{array}\right]) = \left[ \begin{array} {c} cos\theta \\ sin\theta \end{array}\right]$ $T(\left[ \begin{array} {c}0\\ 1 \end{array}\right]) = \left[ \begin{array} {c} -sin\theta \\ cos\theta\end{array}\right]$ $\Rightarrow$ Matrix of linear transformation for vertical shear = $\left[ \begin{array} {c c} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$ 29 |
ApplicationsLinear Transformations have countless applications. Linear Transformations are used in computer graphics for geometric transformations. The translation, rotation and scaling of 2D or 3D objects is performed using linear transformations. 30 |
HistoryIt started when physicists started to use vectors. In 1885, the founder of vector analysis, Oliver Heaviside, came up with an idea of using functions of a vector (linear transformations) in his works on electromagnetism. Later on, a specific term linear mapping or linear transformation came into existence. 31 |
Pause And Ponder
32 |
References
33 |
Further Readinghttps://mathworld.wolfram.com/LinearTransformation.html http://immersivemath.com/ila/ch09_linear_mappings/ch09.html#sec_lm_introduction 34 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
