Velocity and Differentiability |
|---|
DefinitionThe vector function $r(t) = \left\langle x(t), y(t), z(t) \right\rangle$ has a derivative (is differentiable) at $t$ if $x$, $y$, and $z$ have derivatives at $t$. The derivative is the vector function: $$r\prime (t) = \frac{dr}{dt} = \lim_{\Delta t\to 0} \frac{r(t + \Delta t) - r(t)}{\Delta t} = \left\langle x\prime (t), y\prime (t), z\prime (t) \right\rangle$$ For a differentiable vector valued function $r(t) = \left\langle x(t), y(t), z(t) \right\rangle$ representing the position vector of a particle at time $t$, its velocity vector is given as: $$ v(t) = \frac{dr}{dt} = r\prime (t) = \left\langle x\prime (t), y\prime (t), z\prime (t) \right\rangle$$
Bird's Eye ViewWe will be discussing a very specific case of differentiation through the course of these notes: with respect to space curves (which, as we already know, are the set of points $(x(t), y(t), z(t))$, obtained as $t$ varies over a given parameter interval), to analyse how and when we can (and cannot!) differentiate on a given space curve.
Context of the DefinitionFormally, the domain of $f$ is the set of points in the domain of $f$ for which the limit exists, and the domain may be the same or smaller than the domain of $f$. If $f$ exists at a particular $t$, we say that $f$ is differentiable (has a derivative) at $t$. If $f$ exists at every point in the domain of $f$, we call $f$ differentiable. Mathematically, $$r\prime (t) = \frac{dr}{dt} = \lim_{\Delta t\to 0} \frac{r(t + \Delta t) - r(t)}{\Delta t} = \left\langle x\prime (t), y\prime (t), z\prime (t) \right\rangle$$ As we have studied in Equations of Planes and Lines, we know that the slope of a line in $R^{3}$ is given by a direction, rather than a scalar value. The direction vector given by $r\prime (t)$ represents the slope of the curve at a given $t$. 0 |
|
0 |
|
Figure 1: Interpretation of $r\prime (t)$ |
|
There are multiple interpretations of the derivative: 1. Rate of ChangeIf $f(x)$ represents a quantity at any $x$ then the derivative $f\prime (a)$represents the instantaneous rate of change of $f(x)$ at $x = a$. Illustration:
Suppose that the volume of water in a tank for $0\leq t \leq 6 $ is given by $Q(t)=10+5t−t^{2}$
Hint: From Figure 1, we can infer that if the derivative of a function at a given point is positive, the function is increasing.
2. Slope of a Tangent LineThe slope of the tangent line to $f(x)$ at $x=a$ is $f\prime (a)$. The tangent line then is given by, $$y = f(a) + f\prime (a)(x - a)$$ Illustration:
What is the equation of the tangent line to $f(x)= \frac{5}{x}$ at $x=\frac{1}{2}$ ?
3. VelocityThis is a special case of the rate of change interpretation. If the position of an object is given by $r(t)$ after t units of time the velocity of the object at $t=a$ is given by $r\prime (a)$. Illustration:
The position of an object at any time $t$ is given by $s(t) = \frac{t + 1}{t + 4}$
Hint: From Figure 1, we can infer that if the derivative of a function at a given point is zero, the function neither increases nor decreases. Can velocity be obtained for any space curve?A mathematical version of the above question would be: " For a given curve $r(t)$, can the curve be differentiated for any and every value of $t$ in the parameter interval?". This property of the curve is called differentiability. A function can fail to be differentiable at a point if:
The animation given below depicts all three cases. 0 |
|
4 |
|
Figure 2: Non-differentiable curves |
Smooth CurvesA curve $x = f(t), y = g(t)$ is called a smooth curve if $f\prime (t), g\prime(t)$ are continuous and for no value of $t$ are $f\prime (t)$ and $g\prime (t)$ simultaneously equal to zero. The number of continuous derivatives of the position function for a curve to be considered smooth depends on the problem at hand and may vary from two to infinity. To understand this better, consider the following example: $$r(t) = \left\langle t^{2}e^{-t}, 2(t - 1)^{2}\right\rangle$$ Computing $r\prime (t)$, we get: $r\prime (t) = \left\langle 2te^{-t} - t^{2}e^{-t}, 4(t - 1)\right\rangle$ $r_{x}\prime = 0 \implies t = 0, 2$ $r_{y}\prime = 0 \implies t = 1$ Hence, since for a given value of $t$, $r_{x}\prime$ and $r_{y}\prime$ are not simultaneously equal to zero, i.e. $r(t) \neq \overrightarrow{0}$, the given curve $r(t)$ is a smooth curve. Visually, if a curve on zooming in infinitely, looks like a straight line, it is a smooth curve. Zooming in on $\left | x \right |$ at $x = 0$, will always show the sharp corner: 5 |
|
6 |
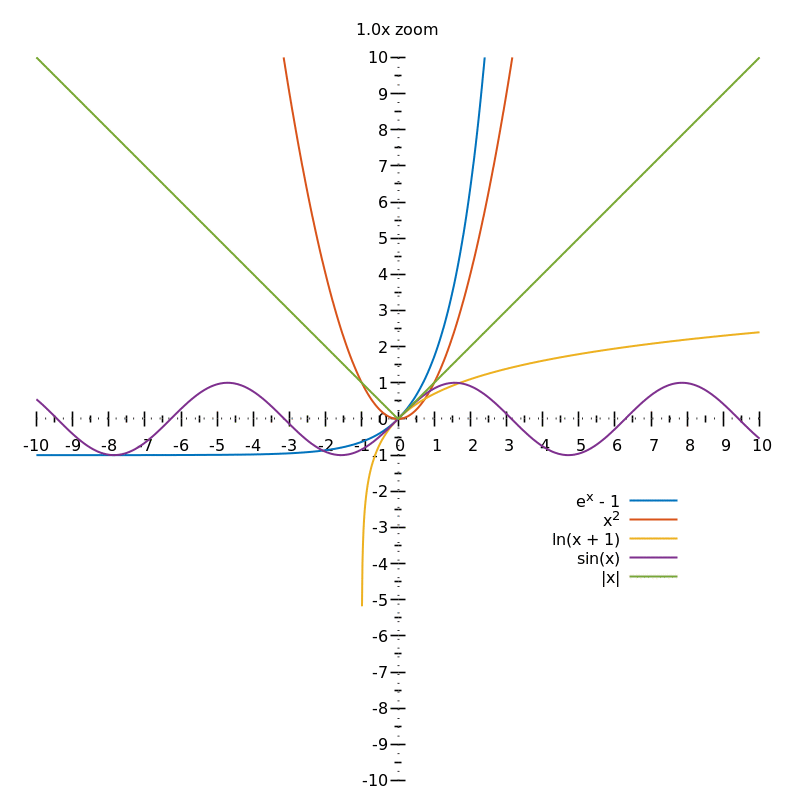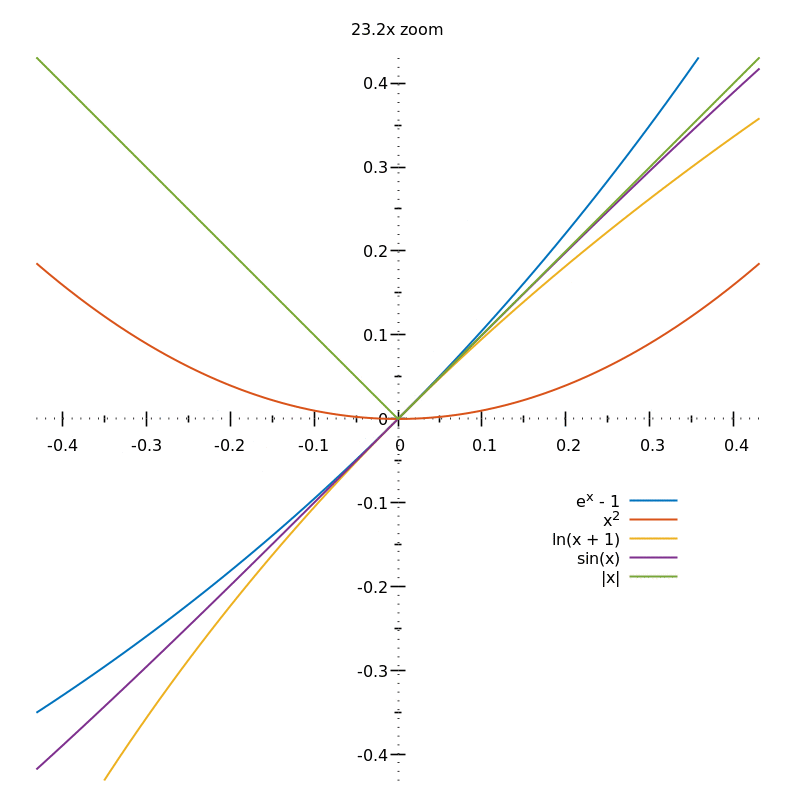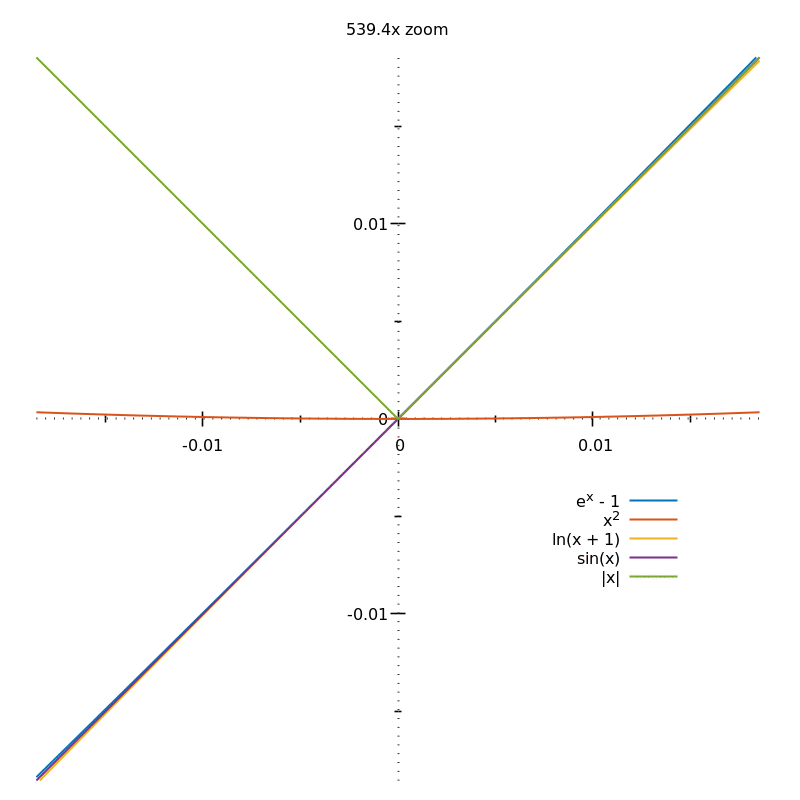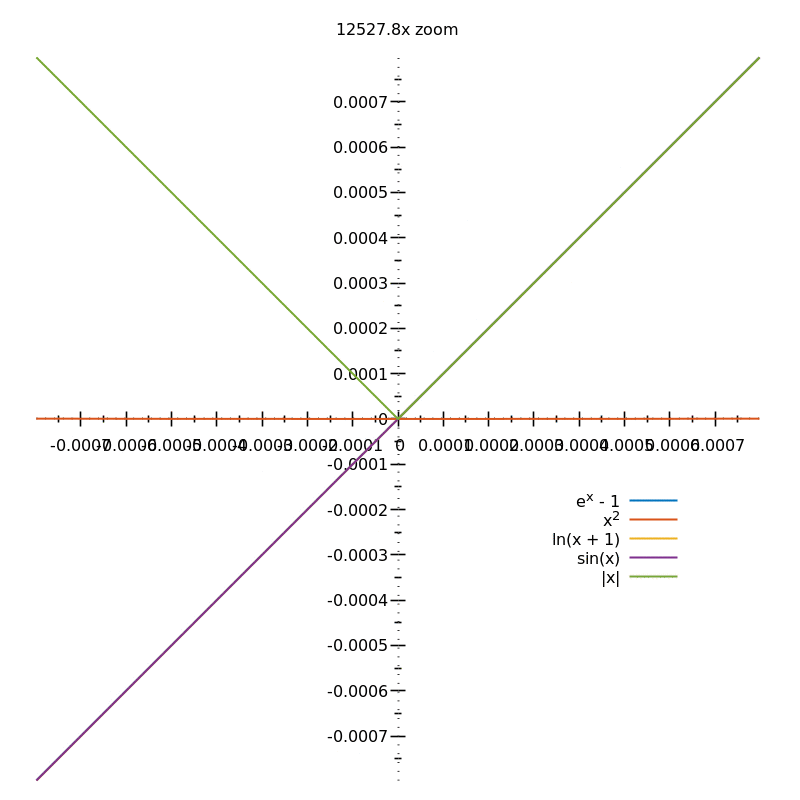
Figure 3: Smooth curves | source: Eric Duminil (https://math.stackexchange.com/users/386794/eric-duminil), Intuitively, why are the curves of exponential, log, and parabolic functions all smooth, even though the gradient is being changed at every point?, URL (version: 2018-05-23): https://math.stackexchange.com/q/2791202 |
Tangent Lines to Space CurvesIf $r(t) = \left\langle f(t), g(t), h(t) \right\rangle$ is a position vector along a curve in $\mathbb{R}^{3}$, then $r\prime (t) = \left\langle f\prime (t), g\prime (t), h\prime (t)\right\rangle$ is a vector in the direction of the tangent line to the curve. Would this mean the velocity vector of a point on a curve is always tangential to the curve? Something to think about. (or not!) Note that it is required that $r(t)\neq\overrightarrow{0}$ to have a tangent vector, as $r(t) = \overrightarrow{0}$ implies that the vector has no magnitude and hence would not give the direction of the tangent. The video below depicts a tangent line to the given space curve at the given point. 7 |
|
8 |
|
Figure 4: Tangent line to a space curve |
Speed and AccelerationAs seen above, the first derivative of the position vector $r(t)$ is called velocity, often denoted by $v(t) = r\prime (t)$. Speed is defined as the length of velocity, i.e. $\left|\left| r\prime (t)\right|\right|$ and is a non-negative scalar. While studying motion of objects, the total acceleration is often broken up as a tangential component, $a_{T}$ and a normal component, $a_{N}$. The tangential component is that part of the acceleration which is tangential to the curve and the normal component is the part of the acceleration normal to the curve. $$a_{T} = v\prime (t) = \frac{r\prime(t)\cdot r\prime\prime(t)}{\left|\left|r\prime(t)\right|\right|}$$ $$a_{N} = k\hspace{0.2cm}\left|\left|r\prime (t)\right|\right|^{2} = \frac{\left|\left|r\prime(t)\times r\prime\prime(t)\right|\right|}{\left|\left|r\prime(t)\right|\right|}$$ where $k$ is the curvature of $r(t)$. The total acceleration is given by: $$a = a_{T}\overrightarrow{T} + a_{N}\overrightarrow{N}$$ where $\overrightarrow{T}$ and $\overrightarrow{N}$ are the unit tangent and unit normal vectors for $r(t)$ respectively. References[1] https://www.ugrad.math.ubc.ca/coursedoc/math100/notes/zoo/continuous.html [2] https://ximera.osu.edu/mklynn2/multivariable/content/02_2_velocity_and_speed/velocity_and_speed [3] https://opentextbc.ca/calculusv1openstax/chapter/the-derivative-as-a-function/9 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
