Equations of Planes and Lines |
|---|
Part 1MotivationWhen we study geometry in $\mathbb{R}^{2}$, all we're really studying is the set of all points whose z-coordinate is zero, i.e., the XY-plane. Through the course of these notes, we will study lines and planes for points whose z-coordinate may not be zero, i.e., in $\mathbb{R}^{3}$. We know that in $\mathbb{R}^{2}$, $y = mx + c$ represents the equation of a line, but does this hold true for $\mathbb{R}^{3}$ as well? -1 |
|
0 |
|
Figure 1: $y = mx + c$ in $\mathbb{R}^{2}$ and $\mathbb{R}^{3}$ |
|
As can be seen from the above video, $y = mx + c$ in $\mathbb{R}^{3}$ represents a plane, as the value of $z$ is not fixed, i.e., it can take any arbitrary value. In this post, we will understand how to generally represent a line and/or a plane in $\mathbb{R}^{3}$. DefinitionThe equation of a plane can be expressed in two forms: Vector Equation: $$\begin{equation}\overrightarrow{n}\cdot(\overrightarrow{r} -\overrightarrow{r_{0}}) = 0\tag{1}\end{equation}$$ where $\overrightarrow{r}$ and $\overrightarrow{r_0}$ are the position vectors of two points lying on the plane, and $\overrightarrow{n}$ is the normal vector to the plane.
Scalar Equation: $$a(x - x_0) + b(y - y_0) + c(z - z_0) = 0$$ often written as $$\begin{equation}ax + by + cz = d\tag{2}\end{equation}$$ where $a, b, c$ are the x-axis, y-axis, and z-axis intercepts respectively and $d = ax_0 + by_0 + cz_0$.
Bird's Eye ViewLet's look into what each of the above forms represents. In the vector form, also called the point-normal form, vector $\overrightarrow{n}$ represents the normal vector, i.e., the vector orthogonal to a plane, while $\overrightarrow{r}$ and $\overrightarrow{r_0}$ represent an arbitrary point and a fixed point lying on the plane respectively. Why do we need the fixed point as well as the normal? Why not one without the other? 0 |
|
0 |
|
Figure 2: Point-normal form of a plane |
|
As can be seen in the above video, the normal vector determines the "tilt" of the plane, while the point fixes the position of the plane along the normal vector.
Looking at the scalar equation, when the equation is written as $\frac{x}{d/a} + \frac{y}{d/b} + \frac{z}{d/c} = 1$, the coefficients of $\frac{1}{x}$, $\frac{1}{y}$ and $\frac{1}{z}$ represent the $x$-, $y$-, $z$- intercepts of the plane respectively. This form is referred to as the intercept form of the equation of a plane. The animation below represents how one such represented plane looks:
0 |
|
0 |

Figure 3: Intercept form of a plane |
Context of the DefinitionNow that we know why both a point as well as a normal vector are required to represent a plane, let us derive these equations, for a better in-depth understanding.
Representing the points $P$ and $P_{0}$ with position vectors $\overrightarrow{r}$ and $\overrightarrow{r_0}$ respectively, we get: 0 |
|
0 |

Figure 4: Plane in $\mathbb{R}^{3}$ |
|
Notice that $\overrightarrow{r} - \overrightarrow{r_0}$ lies completely in the plane. Since the normal vector $\overrightarrow{n}$ is orthogonal to the given plane, it is orthogonal to any vector lying in the plane. Since the dot product of two orthogonal vectors is zero: $$\begin{equation}\overrightarrow{n}\cdot(\overrightarrow{r} - \overrightarrow{r_0}) = 0 \implies \overrightarrow{n}\cdot\overrightarrow{r} = \overrightarrow{n}\cdot\overrightarrow{r_0}\tag{3}\end{equation}$$ This is called the vector equation of the plane. As we know, infinitely many lines pass through a single point unless a direction is specified. Similarly, infinitely many planes pass through a single point in space. Complementarily, a single normal vector will be normal to infinitely many planes. Let us consider an example, to find the equation of a plane whose normal vector is given by $\overrightarrow{n} = \left\langle 1, 1, 2 \right\rangle $ and the point $(1, 2, 3)$ lies on the plane. We know, $\overrightarrow{n}\cdot (\overrightarrow{r} - \overrightarrow{r_0}) = 0$, i.e., $\left\langle 1, 1, 2 \right\rangle\cdot\left\langle\left\langle x, y, z \right\rangle - \left\langle 1, 2, 3\right\rangle\right\rangle = 0$ $\left\langle 1, 1, 2 \right\rangle\cdot\left\langle x - 1, y - 2, z - 3 \right\rangle = 0$ Hence, $(x - 1) + (y - 2) + (2z - 6) = 0 \implies x + y + 2z = 9$ The figure below depicts the plane thus formed, given the above normal vector and fixed point. 0 |
|
0 |
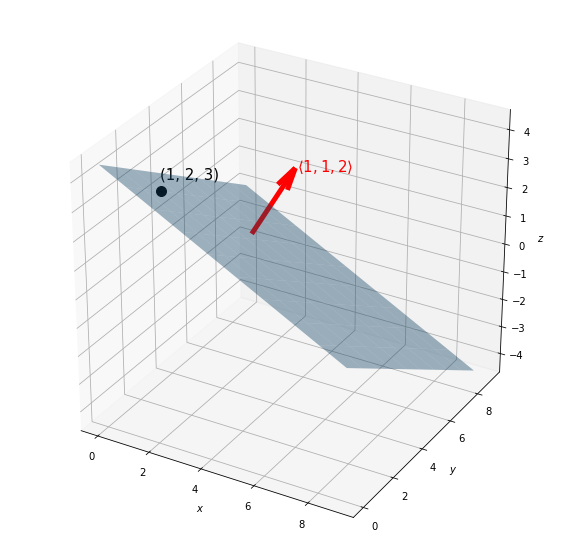
Figure 5: Visualization of plane for given example |
|
Rewriting equation (3), we get:$$\left\langle a, b, c\right\rangle\cdot\left\langle\left\langle x, y, z\right\rangle - \left\langle x_0, y_0, z_0\right\rangle\right\rangle = 0$$ $$\implies \left\langle a, b, c\right\rangle\cdot\left\langle x - x_0, y - y_0, z - z_0\right\rangle = 0 $$ Computing the dot product, we get: $$a(x - x_0) + b(y - y_0) + c(z - z_0) = 0$$ $$ax + by + cz = d$$ Hence, from the vector equation of the plane, we can easily derive the scalar equation. Slightly altering the above equation, we get $\frac{x}{d/a} + \frac{y}{d/b} + \frac{z}{d/c} = 1$, i.e.:$$\frac{x}{a\prime} + \frac{y}{b\prime} + \frac{z}{c\prime} = 1$$ where $a\prime, b\prime, c\prime$ are the x-,y-, and z-axis intercepts respectively. In other words, the plane passes through the points $(a\prime, 0, 0), (0, b\prime, 0)$, and $(0,0,c\prime)$. This is called the intercept form of the equation of a plane.
We noted above that $ax + by + cz = d$ is a plane in space. Using the dot product, let us form a vector from the coefficients on the LHS of the given equation: $$\overrightarrow{n} = a\hat{i} + b\hat{j} + c\hat{k}$$ Using $\overrightarrow{p} = x\hat{i} + y\hat{j} + z\hat{k}$ as the position vector of a point $P(x, y, z)$, the same equation can be expressed as: $$ax + by + c = \overrightarrow{N}\cdot\overrightarrow{p} = d$$ In the special case that $d = 0$, $\overrightarrow{n}\perp\overrightarrow{p}$. In general, for any two points $P_0$ and $P_1$ satisfying equation $(2)$, the vector $\overrightarrow{P_{0}P_{1}} = \Delta\overrightarrow{p} = \overrightarrow{p_1} - \overrightarrow{p_0}$ lies in the plane, and hence satisfies: $$\overrightarrow{n}\cdot\Delta\overrightarrow{p} = \overrightarrow{n}\cdot\overrightarrow{p_1} - \overrightarrow{n}\cdot\overrightarrow{p_0} = d - d = 0$$ Thus, letting the second point $P_1$ be an arbitrary point $P (x, y, z)$ in the plane, we have $$\overrightarrow{n}\cdot(\overrightarrow{r} - \overrightarrow{r_0}) = 0$$ where $\overrightarrow{r}$ and $\overrightarrow{r_0}$ are the position vectors of points $P_1$ and $P_0$ respectively. Through this geometric characterization of a plane from an equation, we understand that the normal vector $\overrightarrow{n}$ determines the "tilt" of the plane, and $d$ picks out, from among the planes perpendicular to $\overrightarrow{n}$, a particular one by determining a point that must lie in the specified plane.
Part 2DefinitionThe equation of a line can be expressed in three forms: Vector Equation: $$\overrightarrow{r} = \overrightarrow{r_0} + \lambda\overrightarrow{v} = \left \langle x_0, y_0, z_0 \right \rangle + \lambda \left \langle a, b, c \right \rangle$$
Parametric Equation: $$\left \langle x, y, z \right \rangle = \left \langle x_0 + \lambda a, y_0 + \lambda b, z_0 + \lambda c \right \rangle$$ Symmetric Equation: $$\frac{x - x_0}{a} = \frac{y - y_0}{b} = \frac{z - z_0}{c}$$ Bird's Eye ViewAs with a line on the coordinate plane, we can find the equation of a line in $\mathbb{R}^{3}$ when given two different points on the line, since subtracting the position vectors of the two points will give the direction vector. Notice in Figure 5, the vector $\overrightarrow{r} - \overrightarrow{r_0}$ represents the subtraction of the two points, and gives the direction vector of the line. Another way is by plotting a single point and a direction vector so that the point passes through it (Animation in Figure 7). Context of the DefinitionIn $\mathbb{R}^{2}$, all we need is the slope and a fixed point on the line to write down the equation. The only difference in $\mathbb{R}^{3}$ is that the equivalent of the slope won't be a simple number, but an orientation! Consider a fixed point $P_{0} = (x_{0}, y_{0}, z_{0})$ on a line, and a vector $\overrightarrow{v} = \left \langle a, b, c \right \rangle$ parallel to said line. Finally, let $P = (x, y, z)$ be an arbitrary point on the line. Representing the points $P$ and $P_{0}$ with position vectors $\overrightarrow{r}$ and $\overrightarrow{r_0}$ respectively, we get:
0 |
|
0 |
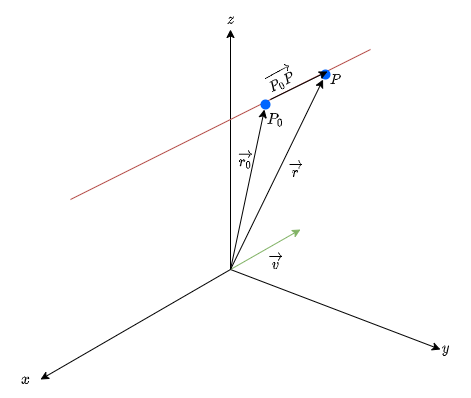
Figure 6: Line in $\mathbb{R}^{3}$ |
|
Notice that we can write $\overrightarrow{r}$ as: $$\overrightarrow{r} = \overrightarrow{r_0} + \overrightarrow{P_0P}$$ Since the vector $\overrightarrow{v}$ is parallel to $\overrightarrow{P_0P}$, we can say: $$\begin{equation}\overrightarrow{r} = \overrightarrow{r_0} + \lambda\overrightarrow{v} = \left\langle x_0, y_0, z_0 \right\rangle + \lambda \left\langle a, b, c \right\rangle\tag{4}\end{equation}$$ This is called the vector form of the equation of a line. Notice how the vector form of the equation of a line is similar to the point-normal form of the equation of a plane. As with the point-normal form of the equation of a plane, the vector equation of a line requires a point as well as its direction.
0 |
|
1 |
|
Figure 7: Vector form of a line |
|
If $\overrightarrow{a}$ is a position vector of a point on the given line in space, and $\overrightarrow{v}$ any vector with direction along the line, the line consists of all the points $\overrightarrow{P}$ given by $\overrightarrow{P} = \overrightarrow{a} + \lambda\overrightarrow{v}$. Note that $\overrightarrow{P}$ lies on the line iff $\overrightarrow{P} - \overrightarrow{a}$ is along the direction of $\overrightarrow{v}$. If the line is to be specified by two points say $A$ and $B$, $\overrightarrow{v}$ can be set as $\overrightarrow{v} = \overrightarrow{b} - \overrightarrow{a}$ in the vector equation, resulting in: $$\overrightarrow{P} = (1 - \lambda)\overrightarrow{a} + \lambda\overrightarrow{b}$$ Hence, we can say that the vector equation of a line includes all the "parameters" required for a line in space to be a line in space. After slightly rewriting equation (4), we get: $$\left\langle x, y, z\right\rangle = \left\langle x_0 + \lambda a, y_0 + \lambda b, z_0 + \lambda c\right\rangle $$ Equating each of these components, the set of equations obtained is called the parametric form of the equation of a line. Since $\lambda$ is a constant term, assuming $a, b, c \in \mathbb{Q} - \{0\}$, we get: $$\frac{x - x_0}{a} = \frac{y - y_0}{b} = \frac{z - z_0}{c}$$ This is called the symmetric equation of a line. What if one of $a, b, c$ happens to be zero? Let’s assume that $a=0$. In this case $\lambda$ will not exist in the parametric equation for $x$. Hence, we will only solve the parametric equations for $y$ and $z$ for $\lambda$. We then set those equal and acknowledge the parametric equation for $x$ as: $$x = x_{0} \qquad \frac{y - y_0}{b} = \frac{z - z_0}{c}$$ IntersectionsThere are three possible outcomes for the intersection of a line and a plane: 1. Line lies completely inside the plane 2 |
|
3 |

Figure 8: Line lies completely inside plane |
|
2. Line is parallel to the plane 4 |
|
5 |
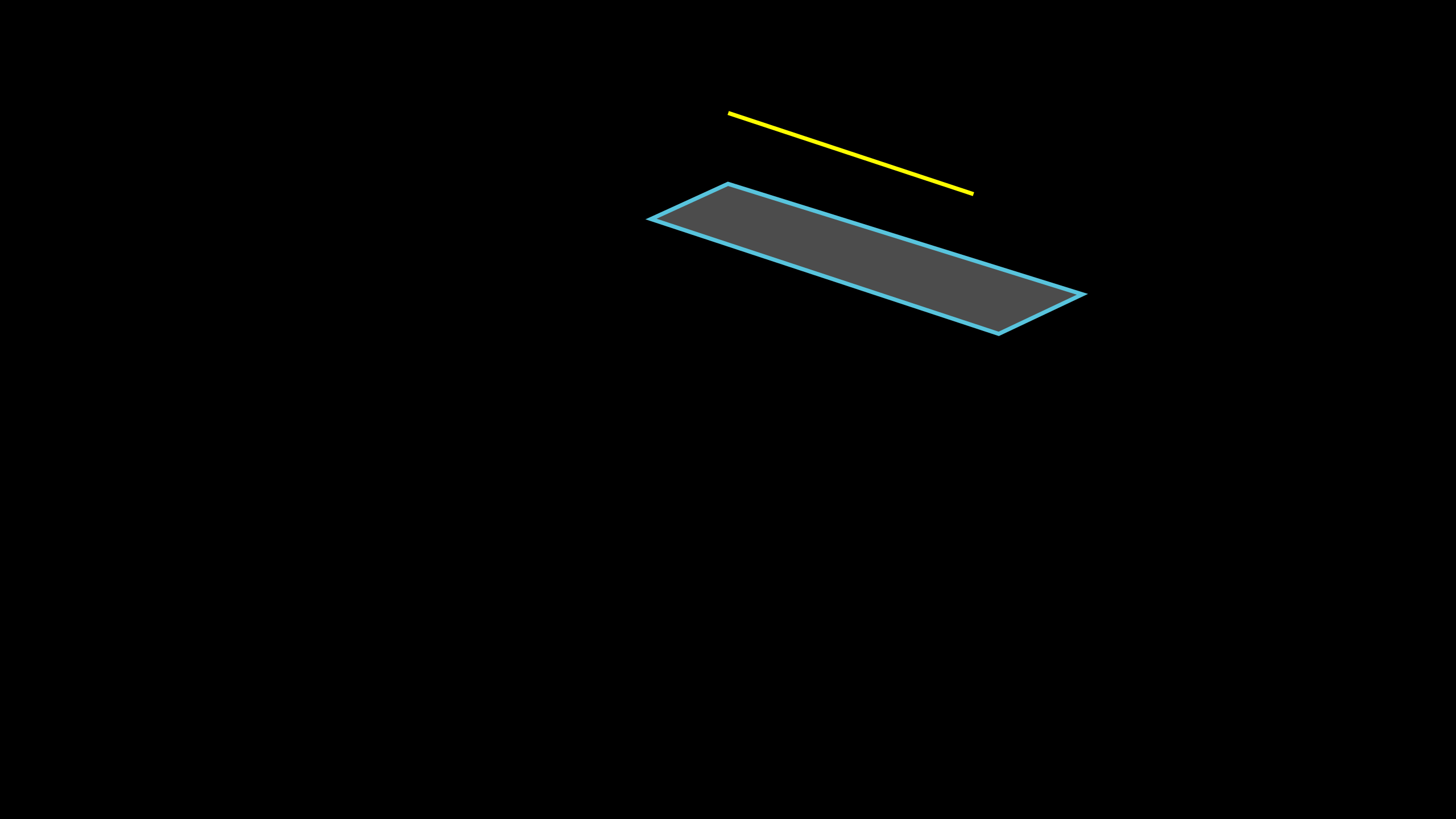
Figure 9: Line is parallel to the plane |
|
3. Line intersects the plane at a single point 6 |
|
7 |
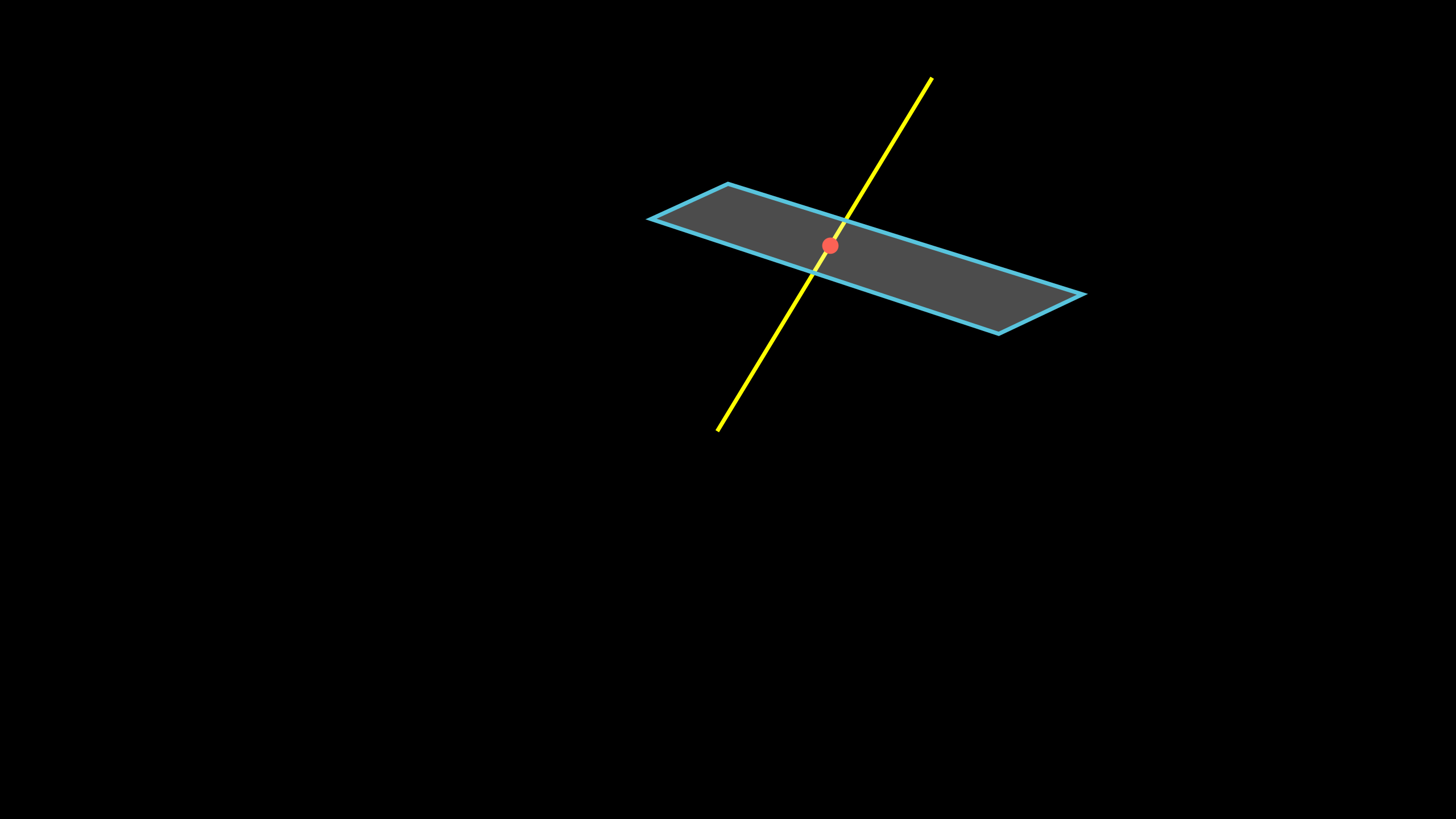
Figure 10: Line intersects the plane at a single point |
|
If the plane is parallel to the line (or if the line is contained in the plane), the normal of the plane and the direction vector of the line will be perpendicular. $\implies \overrightarrow{n}\cdot\lambda\overrightarrow{v} = 0$ If the line is not parallel to the plane, the point of intersection will satisfy the equation of the plane for some value of the parameter $\lambda$; which can be obtained by substituting the parametric equations into the equation of the plane and solving for $\lambda$. In case of the intersection of two lines, the equations of two of the coordinate of each of the lines are equated and solved for $\lambda$. If $\lambda \in \mathbb{R}$, the lines intersect, and the point of intersection can be obtained by substituting this value of $\lambda$. Pause and Ponder
HistoryIn 1637, René Descartes introduced Cartesian coordinates; geometric problems reduced to algebraic problems with numbers; termed analytic geometry, and was applied for spaces < 4 dimensions until the 19th century. Ludwig Schläfli generalized Euclidean geometry to n-dimensional space; discovered all regular polytopes existing in n-dimensional Euclidian spaces. Purely algebraic definition of Euclidian spaces was delineated with the introduction of abstract vector spaces. ApplicationsA diverse variety of applications include:
References[1] http://people.math.harvard.edu/~wboney/fall15/LinesPlanes.pdf [2] https://math.hawaii.edu/~rharron/teaching/MAT203/EquationsOfPlanes.pdf [3] https://tutorial.math.lamar.edu/classes/calciii/EqnsOfLines.aspx [4] https://tutorial.math.lamar.edu/classes/calciii/eqnsofplanes.aspxImages[5] Figure 5 has been generated using Matplotlib. [6] Figure 6 has been generated using draw.io8 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
