Arc Length and Curvature |
|---|
Definition (Arc Length)Arc length is defined as the length along a curve, i.e., for a curve $\overrightarrow{r}(t) = \left\langle x(t), y(t), z(t)\right\rangle$, the arc length from $t = a$ to $t=b$ is given by: $$L = \int_{a}^{b} ds = \int_{a}^{b} \sqrt{(\frac{dx}{dt})^{2} + (\frac{dy}{dt})^{2} + (\frac{dz}{dt})^{2}} \quad dt$$ where $ds$ is the distance along a given curve between two points.
Essentially, $ds$ being the infinitesimal displacement between two points, it can be expressed as $ds = \left| v\right| dt$, where $\left| v\right| = \left|\frac{d\overrightarrow{r}}{dt}\right|$.
Context of the DefinitionFinding the Arc LengthComputing the length of a curve in space is useful for various purposes, for example, if the curve represents the path of a moving object, the length of the curve between two points may be the distance travelled by the object during a certain time period/duration. The animation below depicts how the arc length is computed between two points along a given curve. 0 |
|
0 |
|
Figure 1: What is arc length really? |
|
With reference to the definition of arc length, the value of $ds$ can be calculated as per the following conditions: These variations in $ds$ are given for its simplified calculation. Essentially the same value is being calculated. For example, if $x = y^{4} + 3y^{2}$, it is easier to find $\frac{dx}{dy}$ rather than finding $\frac{dy}{dx}$. We get: $$ds = \sqrt{1 + (\frac{dx}{dy})^{2}}\quad dy = \sqrt{1 +(4y^{3} + 6y)^{2}}\quad dy$$ Computing the arc length $L$ from $y = 1$ to $y = 3$, we get: $$L = \int_{1}^{3}\sqrt{1 +(4y^{3} + 6y)^{2}}\quad dy\approx 104.03173$$ Similarly, if $\overrightarrow{r}(t) = \left\langle r_{x}(t), r_{y}(t)\right\rangle$, it is easier to find $\frac{dr_{x}(t)}{dt}$ and $\frac{dr_{y}(t)}{dt}$.
Definition (Curvature)If $T(t)$ is the unit tangent vector function of a curve $r(t)$, then the curvature $k$ is defined as the rate at which the unit tangent vector changes with respect to the arc length, $s$. Mathematically, $$\kappa = \left|{\frac{d}{ds}(T(t))}\right|$$
MotivationPicture a vehicle driving on a road with (a) a sharp turn (b) a smooth turn. Which of the two turns would be easier for the vehicle to maintain uniform speed? The centripetal force acting on a point on the sharp turn would be lesser than in case of the smooth turn. This would depend on the arc length, as well as the change in the direction of the curve, implying it would depend on its curvature. 0 |
|
1 |
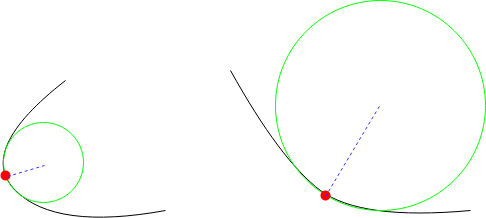
Figure 2: Centripetal forces acting on points on smooth curves | Generated using draw.io |
|
When driving a vehicle on a road, even though a single strip of the road appears to be smooth and continuous, a person inside the vehicle experiences that their upper body shifts/tilts a little due to the centripetal force. This is because the two segments which have been joined together, have different centres of curvature and even though the amalgam appears to be smooth: if the centres of curvature do not coincide, the vehicle would wobble. Bird's Eye ViewIn layman's terms, the curvature measures the rate of change of direction along the curve with respect to length traversed along the curve, i.e., it measures how fast a curve changes direction at a given point. 1 |
|
1 |
|
Figure 3: Simple visualization of curvature |
Context of the DefinitionTo understand the concept of Curvature and how to find its value, we need to first understand the concept of unit tangent vectors. As the name suggests, unit tangent vectors are unit vectors tangential to the curve at certain points. We know that tangent lines / vectors have slopes equal to the instantaneous slope of a curve at a given point, i.e., $$T = \frac{dr}{dt}$$ $$\implies \widehat{T} = \frac{T}{\left|T\right|} = \frac{\frac{dr}{dt}}{\left|\frac{dr}{dt}\right|}$$ Since $\frac{dr}{dt} = v$, the velocity with which a given point on the curve is moving, the absolute value of this velocity vector is the speed vector, i.e., $\left|\frac{dr}{dt}\right| = \frac{ds}{dt}$. Now, considering the unit tangent vector when the curve is expressed as a function of arc length, i.e., $r(s)$ instead of $r(t)$: $$T = \frac{dr}{ds}$$ $$\implies \widehat{T} = \frac{T}{\left|T\right|} = \frac{\frac{dr}{ds}}{\frac{ds}{ds}} = \frac{dr}{ds}$$ As can be inferred from the above equations, $$\kappa = \left|\frac{d^{2}r}{ds^{2}}\right| = \left|\frac{d\widehat{T}}{ds}\right|$$
$$\kappa = \left|\left|\frac{d}{ds}(T(t))\right|\right| = \left|\left|T\prime(t)\frac{dt}{ds}\right|\right|$$ $$\implies \kappa= \frac{\left|\left|T\prime(t)\right|\right|}{\left|\left|\frac{ds}{dt}\right|\right|} = \frac{\left|\left|T\prime(t)\right|\right|}{\left|\left|r\prime(t)\right|\right|}$$ From the definition of $T$, $r\prime = \left| r\prime\right|T$. Using the product rule, $r\prime\prime = \left| r\prime\right|\prime T + \left| r\prime\right| T\prime$. The cross product $r\prime\times r\prime\prime$ is given as: $$r\prime\times r\prime\prime = \left| r\prime\right|T\times \left| r\prime\right|\prime T + \left| r\prime\right|T\times \left| r\prime\right| T\prime$$ $$ = \left |r\prime\right|^{2} (T\times T\prime)$$ $$= \left| r\prime\right |^{2} \left| T\prime\right|$$ $$\implies\left| T\prime\right| = \frac{r\prime\times r\prime\prime}{ \left| r\prime\right |^{2}}$$ Finally, a more practical formula to use can be given by: $$\begin{equation}\kappa (t) = \frac{\left|\left|r\prime(t)\times r\prime\prime(t)\right|\right|}{\left|\left|r\prime(t)\right|\right|^{3}}\tag{1}\end{equation}$$ The animation given below depicts the geometrical interpretation of this formula, and helps us understand that it is not random. 3 |
|
4 |
|
Figure 4: Interpretation of curvature formula |
|
Consider a circle whose vector valued function is given by: $$r(t) = \left\langle R\cos{t}, R\sin{t}, 0\right\rangle$$ Computing the first derivative, we get: $$r\prime(t) = \left\langle -R\sin{t}, R\cos{t}, 0\right\rangle$$ Finally, the second derivative is given by: $$r\prime\prime(t) = \left\langle -R\cos{t}, -R\sin{t}, 0\right\rangle$$ Substituting these values in equation (1), we get $\kappa = \frac{R^{2}}{R} = \frac{1}{R}$ The animation below depicts this scenario of the circle. 5 |
|
6 |
|
Figure 5: Curvature example - circle |
|
The animation given below depicts how the curvature two points along a single curve may have a different value of curvature. Notice how the tangent line to point $P_{1}$ takes longer to travel the first "hump" of the curve, while the second "hump" at point $P_{2}$ is covered at a faster pace. 7 |
|
8 |
|
Figure 6: Different curvature at two points along a single curve |
Pause and Ponder
Applications
References[1] https://tutorial.math.lamar.edu/Classes/CalcIII/Curvature.aspx [2] https://www.whitman.edu/mathematics/calculus_online/section13.03.html [3] https://opentextbc.ca/calculusv3openstax/chapter/arc-length-and-curvature/Images[4] Figure 2 has been generated using draw.io9 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
