Directional Derivatives |
|---|
DefinitionFor the Two-variable The derivative of $f$ at $P_0(x_0, y_0)$ in the direction of the unit vector $\widehat{u} = u_1 \widehat{i} + u_2 \widehat{j}$ is the value $$(D_u f)_{P_0} = \lim_{h \to 0} \frac{f(x_0+h u_1, y_0+h u_2) - f(x_0, y_0)}{h}$$ provided the limit exists.
For the N-Variables Let $f$ be a function on an open set $D$. The directional derivative of $f$ at point $\textbf{r}_0$ in $D$ in the direction of a unit vector $\widehat{\textbf{u}}$ is the limit $$D_{\widehat{u}}f(\textbf{r}_0) = lim_{h \to 0} \frac{f(\textbf{r}_0 + h \widehat{\textbf{u}}) - f(\textbf{r}_0)}{h}$$ if the limit exists
0 |
MotivationLet the function $f(x,y)$ be the height of a mountain range at each point $(x,y)$. If you are standing at some point $(x_0,y_0)$, then the slope of the ground in front of you, will depend on the direction you are facing. It might slope steeply up in one direction, be relatively flat in another direction, and slope steeply down in some other direction. The partial derivative of $f$ in the $x$ direction will give the slope $\frac{\partial f}{\partial x}$ and the slope $\frac{\partial f}{\partial y}$ along the $y$ direction. We can generalize this and can calculate the slope in any direction pointed by the vector $\widehat{\textbf{u}}$ using the directional derivative. 0 |
Bird's Eye ViewThe Directional derivative $D_{\widehat{u}}f(\textbf{r}_0) $ is a value which refers to the rate of change of $f$ at $\textbf{r}_0$ in the direction of $\widehat{\textbf{u}}$. Let us consider the geometrical significance of the directional derivative for a function of two variablesConsider the graph $z = f(x, y)$ over a region $D$. We want to obtain the derivative of the function $f(x,y)$ at $(x_0, y_0)$ along the direction of a vector $\widehat{\textbf{u}}$. For this, we consider the curve obtained by the intersection of the surface $f(x,y)$ and the vertical plane passing through $(x_0, y_0)$, containing the vector $\widehat{\textbf{u}}$. Note that this plane is parallel to the $z$ axis and runs parallel to the unit vector $\widehat{\textbf{u}}$. The curve intersects at the point $P_0 = (x_0, y_0, f(x_0, y_0))$ and the slope of the tangent line to the point along the curve is determined by the directional derivative $D_{\widehat{u}}f(x_0, y_0)$. So, the directional derivative gives the rate of change of $f$ at point $(x_0, y_0)$ in the direction shown by the vector $\widehat{\textbf{u}}$. 1 |
|
3 |
|
Video 1: Geometrical significance of the directional derivative of a function of two variables |
Context of the DefinitionIn the definition of the directional derivative of two variable, the directional derivative at a point $(x_0, y_0)$ gives the differential of the surface in the direction of $\widehat{\textbf{u}}$. The $u_1$ and $u_2$ are the components of $\widehat{\textbf{u}}$ along the $x$ and the $y$ direction. Let us now look at a theorem which provides an alternative approach to understanding and computing the directional derivative of a function at a point. TheoremLet $f$ be a differentiable function of several variable $\textbf{r} = \langle x_1, x_2, \cdots, x_m \rangle$ on an open set $D$ such that the directional derivative of $f$ at a point $\textbf{r}_0$ in $D$ in the direction of unit vector $\widehat{\textbf{u}} = \langle u_1, u_2, \cdots, u_m \rangle$ is $$D_{\widehat{u}}f(\textbf{r}_0) = f'_{x_1}(\textbf{r}_0)u_1+f'_{x_2}(\textbf{r}_0)u_2+ \cdots+ f'_{x_m}(\textbf{r}_0)u_m.$$
The theorem states that the directional derivative for the function of several variables along the direction of vector $\widehat{\textbf{u}}$, is the sum of the partial derivatives of the function $f$ with respect to several variables $(x_1, x_2, \cdots, x_m)$ times the components of the vector $(u_1, u_2, \cdots, u_m)$. Proof:The form used to express the directional derivative in the above function isn't very different from the one using limits (given in the definition). We essentially apply the chain rule to compute the derivative at that point, since $f$ is a differentiable function. Let $f$ be a differentiable function of two variables. We are concerned with the derivative of the function along the vector u at (x0,y0). The parametric equations of the line through $(x_0, y_0)$ and parallel to a unit vector $\widehat{\textbf{u}} = \langle u_1,u_2 \rangle$ for the functions of two variables are $$x(h) = x_0 + h u_1, \hspace{1cm} y(h) = y_0 + h u_2,$$ By the chain rule $$\frac{d}{dh}f(x(h),y(h)) = f'_x(x(h),y(h))x'(h) + f'_y(x(h),y(h))y'(h) $$$$ = f'(x(h),y(h))u_1 + f'(x(h),y(h))u_2 .$$ Substituting $h = 0$ in this relation, we finally get: $$D_{u}f(x_0,y_0) = f'_x(x_0,y_0)u_1 + f'_y(x_0,y_0)u_2.$$ Suppose that $f$ is a differentiable function. By definition, $$D_{\widehat{u}}f(\textbf{r}_0) = \frac{d}{dh}f(\textbf{r}(h))\vert_{h=0}, \hspace{1cm} \textbf{r}(h) = \textbf{r}_0 + h \widehat{\textbf{u}}$$ Similarly, for any number of variables, one has $$\frac{df(\textbf{r}(h))}{dh} = f'_{x_1}(\textbf{r}(h))x'_1(h) + f'_{x_2}(\textbf{r}(h))x'_2(h) + \cdots + f'_{x_m}(\textbf{r}(h))x'_m(h).$$ Substituting $h = 0$ in the above relation and noting that $\textbf{r}'(h) = \widehat{\textbf{u}}$ or $x'_i(h) = u_i$, where $\widehat{\textbf{u}} = \langle u_1, u_2, \cdots, u_m \rangle$, the following result is hence proved. It is crucial to note that the above relation is invalid, if the partial derivatives of $f$ at $\textbf{r}_0$ exist, but $f$ is not differentiable at $\textbf{r}_0$. Unit VectorsWhen a non unit vector $\textbf{u}$ specifies the direction of the rate of change of a function, then dividing it by its length we can obtain the corresponding unit vector $||{\textbf{u}}||$, i.e., $\widehat{\textbf{u}}=\frac{\textbf{u}}{|| {\textbf{u}}||}$. 4 |
ExampleThe function $ f(x,y) = \sqrt{9-3x^2-y^2}$ gives the height of the hill, where the $x$ and $y$ axes moves from west to east and from south to north, respectively. A trekker is at a point $r_0 = \langle 1,2 \rangle$. What is the slope that the trekker sees given that the trekker is facing in the southwest direction.? Solution: A unit vector $\widehat{\textbf{u}} = \langle cos\phi, sin \phi \rangle$ is in the plane, where the angle $\phi$ is along the counterclockwise direction from the positive $x$ axis; i.e. $\phi = 0$points towards the east direction, $\phi = \frac{\pi}{2}$ to the north direction. For the southwest direction the angle should be $\phi = \frac{5\pi}{4}$ and the vector $\widehat{\textbf{u}} = \langle \frac{-1}{\sqrt{2}}, \frac{-1}{\sqrt{2}} \rangle = \langle u_1, u_2 \rangle$. The partial derivatives, $f'_x(x,y) = - \frac{3x}{\sqrt{9 -3x^2 - y^2}}$, $f'_y(x,y) = - \frac{y}{\sqrt{9 -3x^2 - y^2}}$ as these functions are the ratios of continuous functions, the partial derivatives will also be continuous near the point $(1, 2)$ and hence the function $f$ is differentiable at $(1, 2)$. Since $f'_x(1,2) = \frac{-3}{\sqrt{2}}$ and $f'_y(1,2) = \frac{-2}{\sqrt{2}}$, and the slope is given as $D_{u}f(\textbf{r}_0) = f'_x(1,2)u_1+ f'_y(1,2)u_2 = \left( \frac{-3}{\sqrt{2}} \cdot \frac{-1}{\sqrt{2}} \right) + \left( \frac{-2}{\sqrt{2}} \cdot \frac{-1}{\sqrt{2}} \right) = \frac{3}{2} +1 = \frac{5}{2}$. Thus the hiker has to climb up five units of length for every two units of forwarding length as he goes northwest. 5 |
The GradientThe directional derivative of a surface at a point can also be interpreted using the gradient operator. The gradient of a scalar function is an operator which, for each point (x,y) of the domain gives a vector that points in the direction of steepest ascent. The corresponding vector field generated by applying the gradient operator $\nabla$ on a surface $f(x, y)$ is called the gradient field. The gradient operator and vector fields are explained in detail in the coming notes. Definition of gradient Let $f$ be a differentiable function of several variables $r = \langle x_1, x_2, \cdots, x_m \rangle$ on an open set $D$ and let $\textbf{r}_0$ be a point in $D$. The vector whose components are partial derivatives of $f$ at $\textbf{r}_0$, $$\nabla f(\textbf{r}_0) = \langle f'_{x_1}(\textbf{r}_0), f'_{x_2}(\textbf{r}_0), \cdots, f'_{x_m}(\textbf{r}_0) \rangle,$$ is called the gradient of $f$ at the point $\textbf{r}_0$.
The gradient for a two-variable functions is a two-dimensional vector given as: $$f(x,y): \hspace{1cm} \nabla f= \langle f'_{x}, f'_{y}\rangle;$$ The gradient for a three-variable functions is a three-dimensional vector given as: $$f(x,y,z): \hspace{1cm} \nabla f= \langle f'_{x}, f'_{y}, f'_{z}\rangle;$$
6 |
Calculation and GradientsWe now develop an efficient formula to calculate the directional derivative for a differentiable function $f$. We begin with the line $$x = x_0 + su_1, \hspace{1cm} y = y_0 + su_2,$$ through $P_0(x_0, y_0)$, parametrized with the arc length parameter $s$ increasing in the direction of the unit vector $\textbf{u} = u_1 \textbf{i} + u_2\textbf{j}$. Then by the Chain Rule we find, $$ \left( \frac{df}{ds} \right)_{u P_0} = \left( \frac{\partial f}{\partial x} \right)_{P_0} \left( \frac{dx}{ds} \right) + \left( \frac{\partial f}{\partial y} \right)_{P_0} \left( \frac{dy}{ds} \right) \hspace{1cm} \text{Chain Rule for differentiable } f$$ As $\frac{dx}{ds} = u_1$ and $\frac{dy}{ds} = u_2$, $$= \left( \frac{\partial f}{\partial x} \right)_{P_0}u_1 + \left( \frac{\partial f}{\partial y} \right)_{P_0}u_2 $$$$=\underbrace{\left[ \left( \frac{\partial f}{\partial x} \right)_{P_0}\textbf{i} + \left( \frac{\partial f}{\partial y} \right)_{P_0}\textbf{j} \right]}_{\text{Gradient of } f \text{ at } P_0} \cdot \underbrace{\left[ u_1\textbf{i} + u_2 \textbf{j} \right]}_{\text{Direction }u}$$ Thus, the Directional Derivative is a Dot Product and it states that: If $f(x, y)$ is differentiable in an open region containing $P_0(x_0, y_0)$, then $$ \left( \frac{df}{ds} \right)_{u P_0} = (\nabla f)_{ P_0}\cdot \textbf{u}$$ the dot product of the gradient $\nabla f$ at $P_0$ and $\textbf{u} $. In brief, $D_{u }f = \nabla f\cdot \textbf{u}$.
7 |
Properties of the Directional Derivative $D_{u }f = \nabla f\cdot \textbf{u} = |\nabla f|\cos\theta$1. When $\cos \theta = 1$ or when $\theta = 0$, the function $f$ increases extremely in the direction of $\nabla f$. That is for every point $P$ in its domain, $f$ increases rapidly along the direction of the gradient vector $\nabla f$ at $P$. This is the direction of steepest ascent. The derivative in this direction is $$D_{u }f = |\nabla f|\cos(0) = |\nabla f|.$$ 2. Similarly, $f$ decreases extremely in the direction of $\nabla f$. This is the direction of steepest descent. The derivative in this direction is $$D_{u }f = |\nabla f|\cos(\pi) = -|\nabla f|.$$ 3. At any other direction $\textbf{u}$ orthogonal to a gradient $\nabla f \neq 0$, which is in the direction of zero change in $f$ because $\theta$ equals $\frac{\pi}{2}$ and $$D_{u }f = |\nabla f|\cos(\frac{\pi}{2}) = |\nabla f|\cdot 0 = 0.$$ 8 |
|
9 |
|
Video 2: The gradient indicates the maximum and minimum values of the directional derivative at a point |
Gradients and Tangents to Level CurvesAt every point $(x_0 , y_0)$ in the domain of a differentiable function $f(x, y)$, the gradient of $f$ is normal to the level curve through $(x_0 , y_0)$.
10 |
|
10 |
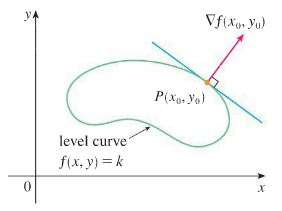
Figure 1: A function of two variables, the gradient is normal to the level curves, $f(x,y)=k$. [1] |
|
11 |
|
Video 3: Gradient to the Level Curves in the direction to the steepest ascent |
Functions of Three VariablesFor a differentiable function $f(x, y, z)$ and a unit vector $\textbf{u} = u_1\textbf{i} + u_2 \textbf{j} + u_3 \textbf{k}$ in space, we have $$\nabla f = \frac{\partial f}{\partial x} \textbf{i} + \frac{\partial f}{\partial y} \textbf{j} + \frac{\partial f}{\partial z} \textbf{k}.$$ and $$D_{u}f = \nabla f \cdot \textbf{u} = \frac{\partial f}{\partial x} u_1 + \frac{\partial f}{\partial y} u_2 + \frac{\partial f}{\partial z} u_3.$$ The directional derivative can once again be written in the form $$D_{u}f = \nabla f \cdot \textbf{u} = |\nabla f||u| \cos \theta = |\nabla f|\cos \theta,$$ At any given point, $f$ increases excessively in the direction pointed by $\nabla f$ and excessively decreases in the direction pointed by $-\nabla f$. The derivative is zero in any other direction which is orthogonal to $\nabla f$, . 11 |
ApplicationsDirectional Derivatives1. The directional derivative is used in fields where vector analysis applies, such as electromagnetic theory, fluid dynamics, elasticity, mechanics, etc. 2. They can be used in determining the rate of switching inputs in production functions, which can be very helpful in determining / forecasting switching costs for a given bundle of inputs. 12 |
|
13 |
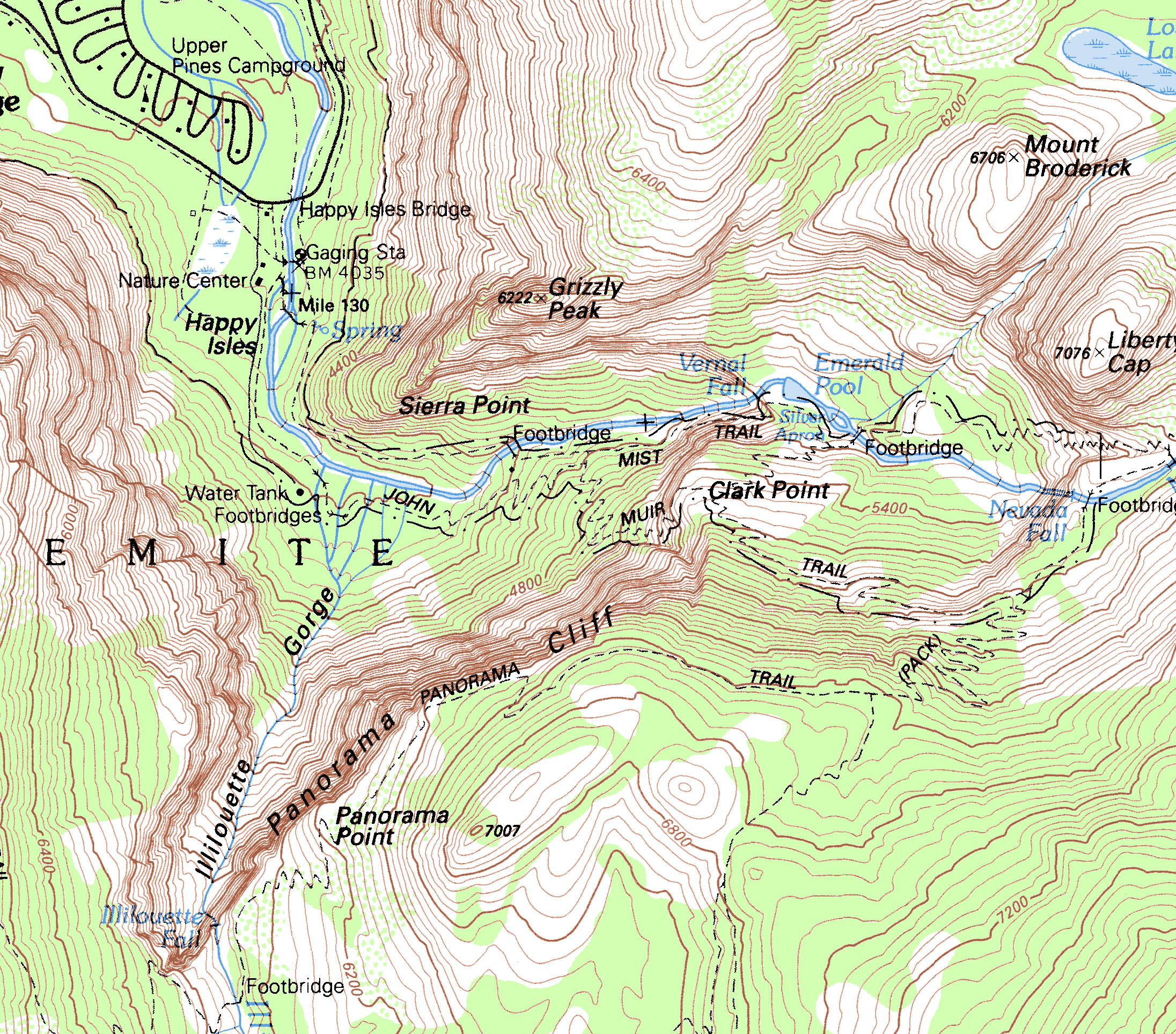
Figure 2: Contours within Happy Isles and Mist Trail area in Yosemite Valley show streams, which follow paths of steepest descent, running perpendicular to the contours. [2] |
Pause and PonderWhy gradients are used to find the maxima and minima in a multivariable function? 14 |
|
15 |
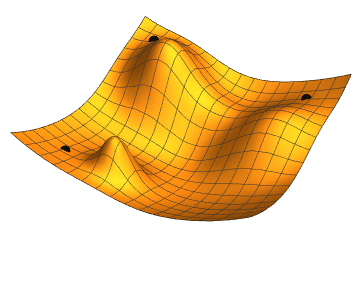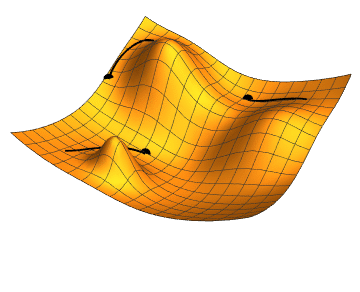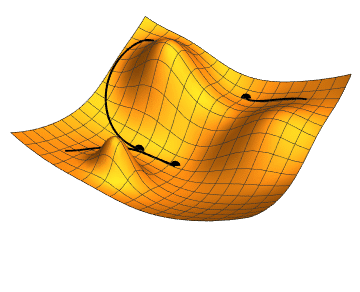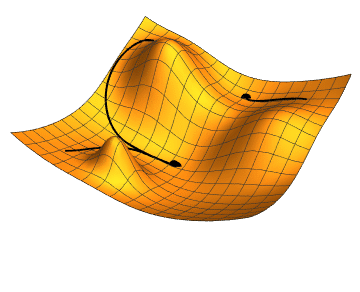
Figure 3: Gradients moving to different minimas in the surface [3] |
References1. Nykamp DQ, “An introduction to the directional derivative and the gradient.” From Math Insight. http://mathinsight.org/directional_derivative_gradient_introduction 2. https://people.clas.ufl.edu/shabanov/files/calculus3_2019Chp3.pdf 3. Book - Thomas’ Calculus Early Transcendentals 16 |
Figures[1] Reproduced from https://zeno.boisestate.edu/notes/275/figures/gradient2-1.png [2] Reproduced from https://commons.wikimedia.org/wiki/File:Happy-Isles-topo-map.jpg [3] Reproduced from Jacopo Bertolotti / CC0 https://commons.wikimedia.org/wiki/File:Gradient_descent.gif 17 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
