Vector Fields |
|---|
DefinitionA vector field on a domain in the plane or in space is a function that assigns a vector to each point in the domain. A field of three-dimensional vectors is like -
$$\vec F(x,y,z)= M(x,y,z)\hat i + N(x,y,z)\hat j +P(x,y,z)\hat k $$The field is continuous if the component functions $M,N,P$ are continuous , differentiable if $M,N,P$ is differentiable, and so on. A field of two dimensional vectors is like$$\vec F(x,y)= M(x,y)\hat i + N(x,y)\hat j $$. [1] More generally Vector field is defined as -- If $D$ is a set in $\mathbb R^n$, a vector field on $\mathbb R^n$ is a function $\vec F$ that assigns vector $\vec F(x_1,x_2\cdots x_n)$ at each point($x_1,x_2,\cdots x_n$) in $D$. 1 |
MotivationVectors have a direction and a magnitude - for instance, an arrow can be considered as a vector. But, what is a vector field? Imagine a leaf floating in the wind, now imagine that at any given instant what factors decide the leaf's position at the next moment? Obviously, there has to be some force (vector) that will drive it to a next position with velocity, the same thing will repeat for later moments and as a result, the leaf will float in the air along some path. From this example, we can deduce that at every point in the air there is some force vector associated which "tells" the leaf where it has to go next. Here the Vector field can be thought of as the set of force vectors all in the air determining the path of the leaf. In a more systematical study of fluid flow, electromagnetic fields, and so on, we need the vector fields to calculate work done along a path or flux through an area. It has tremendous applications in constructing real-time wind maps, water currents in oceans, and also in vector graphics animation, topographical map matching & manipulation, and so on. 2 |
Bird's Eye ViewGeometrically, vector field means that for every point in a region we assign a vector. In other words, at every point in the input space (domain), a vector is attached - which represents the output (range). For example, consider the following animation, where $F(x,y) = -y \hat{i}+x\hat{j}$. We can see that at every point in the 2D plane we plot a vector (of course we space it out and scale it down to avoid illegibility); same goes for the 3D vector field - not only we assign a vector at each point in the plane, but also at every level. 3 |
|
4 |
|
Animation 1 : Two-dimensional and Three-dimensional Vector Fields |
|
There is also another type of vector field named gradient vector field. This is just like any other vector field but the difference is in the process how it is generated, and it also has some striking properties. You can generate it from a scalar function $f$ by applying "$grad$" operator($\vec \nabla$) on it. 5 |
|
The field generated in such a way is also named "Conservative Field" and doing Line Integrals in this type of field is very easy (See 'Fundamental Theorem for Line Integrals').
6 |
Context of DefinitionA vector field is generated by a vector function which take values at a point$(x_i,y_i)$ to construct out a vector$\vec F(x_i,y_i)$, and then the constructed vector is shifted to that point$(x_i,y_i)$. 7 |
|
10 |
|
Animation 2 : Construction of a vector field |
|
If you observe a vector function, it just consists of scalar functions associated with different directions. The vectors are associated with each point in space but for obvious reasons, they all are not drawn in the pictures. Sometimes vector notation is used entirely for describing a vector field by replacing the coordinates($x,y,z$) with their position vector($\vec r$). For inverse square fields like Gravitational field and electromagnetic field, it is customary to use $\vec r$ instead of $x\hat i+y\hat j+z\hat k$. Now, $$\vec F(x,y,z)= \dfrac{k}{(x^2+y^2+z^2)} (x\hat i+y\hat j+z\hat k) \quad \text{or,}\quad \vec F(\vec r) =\dfrac{k}{r^2} \vec r$$ Which one is easier/prettier to deal with? 12 |
♦ Gradient Vector fieldsThis is an important and interesting type of vector field. Gradient gives the direction and magnitude of the steepest change of a scalar function at every point. We will understand it with the help of an example. 13 |
|
17 |
|
Animation 3 : Gradient of a scalar function is a vector field. |
|
Consider a region where the pressure at every point is defined by scalar function $P(x,y,z)$. To construct the gradient vector field from it you go to every point in the region and find the direction and magnitude of the largest increase in pressure which is a vector. This work is done by the gradient operator. Now we see an example with the function $f(x,y,z)=x^2yz^3$. Its gradient is, It is indeed a vector field. For a point $(1,1,1)$ we get a vector $2\hat i+\hat j+3\hat k$, which gives us the direction and magnitude ($\sqrt{2^2+1^2+3^2}=\sqrt 14$) of the maximum rise in the value of the function at the neighborhood of that point. The vectors in the gradient vector field are always perpendicular to the contour lines of the scalar field. To use the advantages of this type of field see the 'Gradient theorem' and 'conservative fields'. Vector fields are nicely drawn by the help of computers but one can also draw two dimensional and some of the three-dimensional fields by hand making a table of data.
Applications
19 |
|
21 |
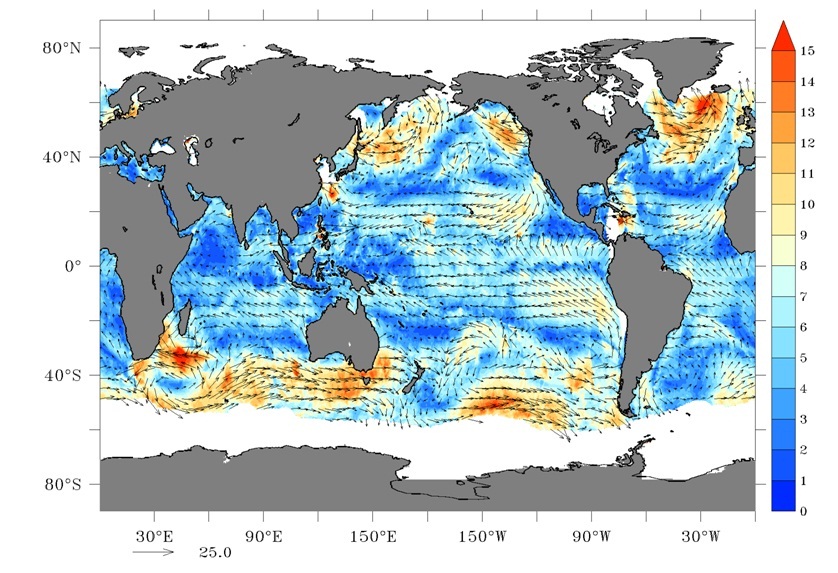
A global wind map over oceans from SCATSAT-1 mission of ISRO, source :https://www.isro.gov.in/pslv-c35-scatsat-1/scatsat-1-other-products, SCATSAT-1 Winds (m/s) Global Coverage – 3rd and 4th Oct, 2016 |
|
3. Sometines in the process of solving first-order differential equations slope field[8](somewhat similar to the vector field) is generated, merely to get the feel for what a solution should be before one head to the explicit general solution. 25 |
|
25 |
|
Animation 4 : Generating a slope field. |
|
4. To construct streamlines in a fluid and study it, the velocity vector field is generated. 5. The concept of Vector field is also used in epidemiology, population studies and Image Processing, animation[6,7]. 26 |
HistoryNewton extensively worked with vectorial entities (e.g., velocity, force), but never made significant calculus of vectors. In the 19th and early 20th century, the systematic study and use of vectors started[9]. In 1843, in a very dramatic manner, Hamilton discovered "quaternions", which he described in a letter to his son in 1865. Hamilton's discovery was epoch-making and that may be compared to the discovery of non-Euclidean geometry. Next in a paper published in July 1846, issue of "Philosophical Magazine"(5,29;26-31) Hamilton coined the term "Vector"[10], later he also introduced the $\vec \nabla$ operator. 'Maxwell divided the variables of physics into two categories, scalars and vectors and popularized the idea of quaternions in his Treatise on Electricity and Magnetism. Gibbs was introduced to quaternions when he read Maxwell's Treatise on Electricity and Magnetism. He concluded that vectors would provide a more efficient tool in physics... 1881, Gibbs privately printed notes on vector analysis for his students, which were widely distributed to scholars in the United States, Britain, and Europe. The first book on modern vector analysis in English was Vector Analysis (1901)... Oliver Heaviside (1850--1925), a self-educated physicist who was greatly influenced by Maxwell, published papers and his Electromagnetic Theory (three volumes, 1893, 1899, 1912) in which he attacked quaternions and developed his own vector analysis. Heaviside had received copies of Gibbs's notes and he spoke very highly of them. In introducing Maxwell's theories of electricity and magnetism into Germany (1894), vector methods were advocated and several books on vector analysis in German followed. Vector methods were introduced into Italy (1887, 1888, 1897), Russia (1907), and the Netherlands (1903). Vectors are now the modern language of a great deal of physics and applied mathematics and they continue to hold their own intrinsic mathematical interest.'[9]
28 |
Pause and PonderWe represented $f(x,y)$ as a 3-D surface with the help of $z$ axis but we can also represent it in 2-D by the help of different colours. Is there any way to represent higher dimensional vector fields? With the help of the wind map data, visualized by vector fields, peoples lives are saved. A quote from ISRO's scatsat-1 mission page: 29 |
References
Further Reading
30 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
