Fubini's Theorem |
|---|
DefinitionFor double integral of a function $f(x,y)$ in a rectangular region $R=[a, b]\times [c, d]$ we can write, $$\int_R f(x,y)\ dxdy = \int_a^b\left(\int_c^d f(x,y)\ dx\right)dy = \int_c^d\left(\int_a^b f(x,y)\ dy\right)dx$$
if $\iint_R |f(x,y)|\ dxdy < \infty$, otherwise the integral value is infinite.
Extension for multiple integrals, If $f$ is a function integrable on $R^n$ and $\int_{R^n}|f\ |dx^n < \infty$ then a multiple integral can be done by dividing it into single integrals (iterated integrals), $$\int_{R^n}f(x_1,x_2\cdots x_n )dx^n= \int\left(\cdots \left(\int f(x_1\cdots x_n )dx_1\right)\cdots \right)dx^n$$
Here we can do $x_1\cdots x_n$ integration in any order if the subsequent integrands become integrable. While we integrate over one variable the others act as constants.
-1 |
MotivationWe integrate a function of a single variable easily but how do we integrate functions of more than one variable? We have Riemann Sum method to get the numerical value of any integral if the region is well defined, but for higher dimensions, it has limitations/difficulties. So for doing a multiple integral by hand we have no other way than dividing it into single variable integrals and do them recursively (iterated integrals[3]) by means of some methods and anti-derivative formulas. It gives two different answers($-\frac{\pi}4$ and $\frac{\pi}4$) for two different order of iteration(first $x$ or first $y$ integration). So it is not obvious that the iteration method gives us the right answer always! In the current topic, we will see how to check if an integral can be done by the method of iteration; we will also see how to take advantage of different orders of iteration. -1 |
Bird's Eye ViewFubini's Theorem gives the conditions under which it is possible to compute a integral as an iterated integral. Double integral is the "smallest" multiple integral where we can use this theorem. If we have a double integral as $\int_a^b\int_c^d f(x,y)\ dxdy$ over a rectangular region $R=[a, b]\times [c, d]$ then we can write, If the above equalities are valid, we can either do the $x$ integral or the $y$ integral first, but that may not be always possible!
0 |
Context of the DefinitionIn general, we can't do multiple integrations by iterations until some conditions are fulfilled. Fubini's theorem gives us these conditions[1,5],
Now we see an example where changing the order of integration gives different values-- Method 1 : First we do the $x$ integration , \begin{align} \int_0^1 \dfrac{x^2-y^2}{(x^2+y^2)^2} dx &=\int_0^1 \dfrac{-(x^2+y^2)+2x^2}{(x^2+y^2)^2} dx \\ Method 2 : First we do the $y$ integration, \begin{align} \int_0^1 \dfrac{x^2-y^2}{(x^2+y^2)^2} dy &=\int_0^1 \dfrac{(x^2+y^2)-2y^2}{(x^2+y^2)^2} dy \\ We see that in the previous two possible iteration of the given double integral we get different answers. Here fubini's theorem implies that $$\int_0^1\int_0^1\left|\dfrac{x^2-y^2}{(x^2+y^2)^2}\right| dxdy=\Large\infty$$ 0 |
|
0 |
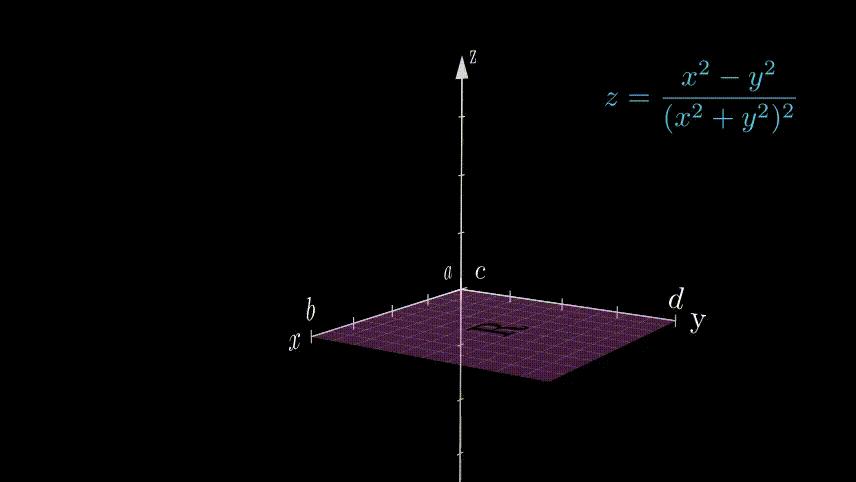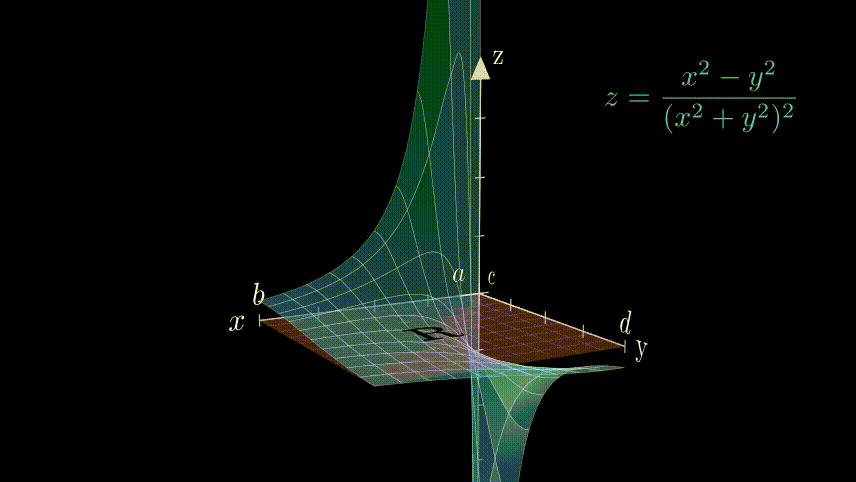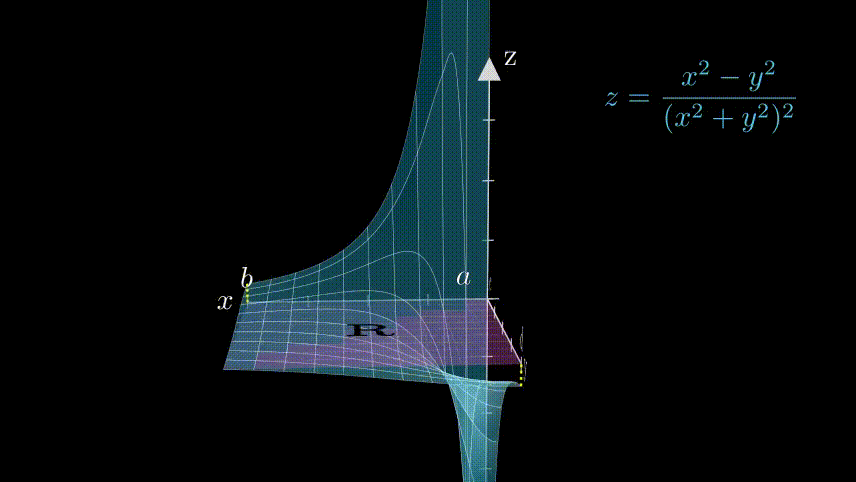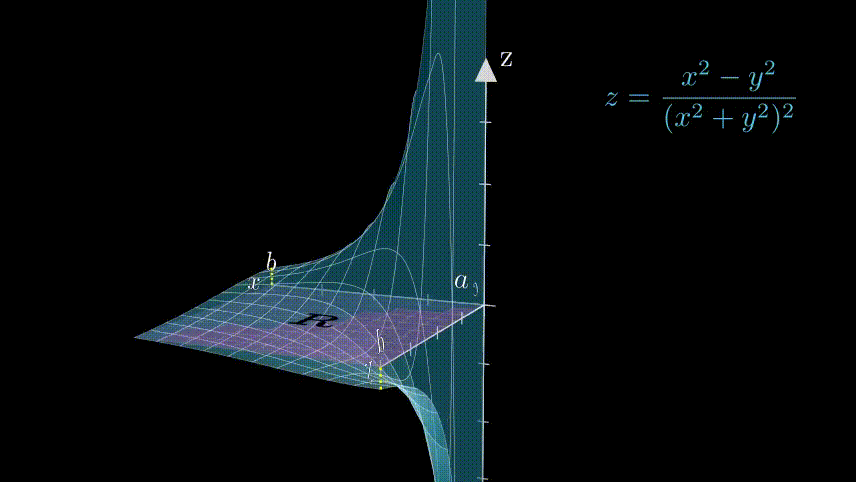
Animation 1: Nature of the Function $\dfrac{x^2-y^2}{(x^2+y^2)^2}$. The blowing up of the function near the origin gives insight about the calculated results. |
♦ Fubini's theorem over general regionsIf we have to set double integral of the function $f(x,y)=xy$ in closed region $R$ between the curves $y=x^2$ and $y=x$, it would be like-- 0 |
|
0 |
|
Animation 2: The function $z=xy$ and the region of integration $R$ |
|
We see that function is a good one i.e. no singularities[8] in the region of integration- no infinities. So we can change the order of integration as we want.. Method 1Here we first do the $y$ integration. Someone can say why the limit is not like $\int_{y=x}^{x^2}$. It is not so because if you draw the region you will see $y=x^2$ is closer to $x$ axis so it has to be the lower limit of the integration. But if someone has mistakenly done it, he/she has to multiply with a negative sign everywhere. Method 2Here we first do the $x$ integration. Observe the limits of integration, The two methods give the same result as expected .
0 |
|
0 |
|
Animation 3: The two methods of iteration for the double integral. |
|
So to conclude we cannot always do a multiple integral by the method of iterations, for doing so we have to "get permission from Fubini(Fubini's theorem)!". After checking the function if he says "I am pleased with the function's behavior in the integration region", then we can do the iterated integral without any fear of invalid answer.
Applications
2. In a quite similar way, if we have some boundary curve like shown in the below Figure, we can change the order of integration as needed as long as the integral respects the fubini's criteria for iterability. 0 |
|
0 |
|
Animation 4: Setting limits in a curvy region. |
|
3. To evaluate the value of Gaussian integral- which is one of the most useful and elementary integrals, we use Fubini's theorem. 4. Another standard application of Fubini’s theorem is the inversion formula for Fourier transform. 0 |
HistoryThe special case of Fubini's theorem was known to Leonhard Euler in the 18th century. In 1904 Henri Lebesgue extended this to bounded measurable functions on a product of intervals. In 1906 Levi proposed an extension of the theorem to functions that were integrable rather than bounded, and this was proved by Fubini in 1907, known as "Fubini's Theorem". In 1909 Leonida Tonelli gave a variation of Fubini's theorem.
0 |
Pause and PonderDid you find any similarities between partial differentiation and the iteration method in integration? Fubini's theorem was formulated in 1907 but people have done multiple integrals before that, how? (See Cavalieri's Principle) Is there any situation where Fubini's theorem fails? This theorem is rigorously proved by measure theory. You should know that doing multiple integrals in higher dimensions by hand is most of the times very laborious/utterly difficult, so people prefer to do it by some numerical methods over computers where we don't need Fubini's theorem, one such widely used numerical method is Monte-Carlo method[10]. 0 |
References
0 |
Further Reading
0 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
