Conservative Fields, Path Independance, Gradient Fields |
|---|
DefinitionsConservative Field
(Three equivalent definitions of the conservative field are mentioned below) A vector field F is conservative if a line integral of F along any curve C is path independent. A vector field F is conservative if for any closed curve C in the domain of F, the line integral $\oint _{C}F.ds = 0$. A vector field F is conservative if it is the gradient for some function f. Closed Path A path C is closed if it starts and ends at the same point. Path Independence A vector field F is path independent if for any two oriented curves $C_{1}$ and $C_{2}$ in the domain of F with common initial point P and terminal point Q, $\int _{C1}F.ds = \int _{C1}F.ds$ Gradient Field A vector field F is a gradient field if there exists a scalar-valued function f(x,y,z) defined on the entire domain of F such that $\nabla f = F$ 2 |
MotivationThe function of a flight of stairs, one of mankind's earliest and most elementary architectural inventions, is to make covering vertical distances easier. Technically speaking, a foundational aspect of its design (assuming that we're going up) is that if step b succeeds step a, then step b is higher than step a, and is consequently at a higher gravitational potential than a. In other words, with every step you take on a flight of stairs, you are overcoming more gravity and simultaneously gaining more gravitational potential. Consider then Fig 1 that follows. They illustrate a famous illusion, the Penrose Stairway. In both depictions, the stairs appear infinitely circular and disregard the rule of stair n+1 being at a greater gravitational potential than stair n. The Penrose Stairway is aptly termed an Impossible Figure. What makes it impossible is a basic property of the gravitational field - that it is a conservative field. 3 |
|
4 |
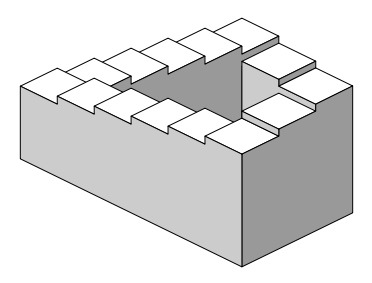
Figure 1: The Penrose Stairway is an impossible figure created by Lionel Penrose and his son Roger Penrose. |
Bird's Eye ViewPicture two roads winding up a hill. One is shorter and much steeper than the other gradually sloping one. The laws of physics guarantee that regardless of the road you take to the top, the work done by you is the same. How is it possible that taking a steeper path expends the same energy (in terms of physical work) as taking a gradually sloping path? Such a result indicates that the nature of the path chosen is of no consequence, or in other words, the work done is path independent. Path independence, defined usually for a field, suggests another important fact - that it is conservative. This is seen in the above example - work is done against gravity and its value is independent of path. So, when is path considered conservative? Additionally, what does it conserve? The following sections assist us in answering such questions. 5 |
|
5 |
|
Animation 1: The gravitational field is conservative, which is why when measuring the work done, the path taken from a point of lower altitude to one at a higher altitude is of no consequence. |
Context of the DefinitionAccording to its definition, a conservative field must satisfy any one of these three conditions-
Ley's revisit the concepts of line integration and the Fundamental Theorem of Line Integrals before proceeding with conservative fields. We will begin with a brief recap of these concepts (which are thoroughly discussed in a previous lecture note) The line integralThe line integral is given by the formula $\int_{C} \vec F . dr$. Let's break this down -$\vec F$ is a vector field of a function f, defined on the plane. C is a curve, oriented counter-clockwise. Suppose you are moving along the curve C. The vector $\vec dr$ gives you the direction you are facing at a point. The relative orientation between your direction and the direction the vector field at that point is given by the dot product $\vec F \cdot \vec dr$. Integrating this dot product measures this relative orientation along the entire curve. If you were swimming along a curve and the vector field F was represented by fluid flow, the line integral would measure upto what extent the water is flowing with you versus against. The line integral is used to measure the physical work done. In mechanics, this would be the gravitational work, whereas in electrostatics, this would be the electrostatic work done. The animation below explains the line integral. 7 |
|
8 |
|
Animation 2: Breaking down of the formula of the line integral |
The Fundamental Theorem of Line IntegralsThe Fundamental Theorem of Line Integrals states that, for a vector field F of a function f which is computed along a curve C with wnd points A and B, $\int_{C} \vec F \cdot \vec dr = f(B) - f(A)$
Now that we are equipped with the prerequisites, we may move on to conservative fields. Path IndependenceA vector field is considered path independent if the value of its line integral depends solely upon the end points of the curve defined in it. Recall the example of the gravitational field, in which work done, or energy expended was dependent on on the end points, rather than the entire path itself. The line integral is used to measure the work done in a system. If the field is path independent, then the value of the line integral must be the same regardless of the path taken. This follows from the Fundamental theorem for line integrals which emphasises that on a path independent vector field, the integral of the rate of change is equivaent the net change. Animation 2 presents the case of a path independent field, whereas animation 3 shows a path dependent field.
9 |
|
10 |
|
Animation 2: Line integrals in a path independent vector field |
|
11 |
|
Animation 4: Line integrals in a path dependent field |
|
A path independent vector field has an interesting property - that in a path independent vector field, the line integral of a closed loop will always equal 0. This can be proven using the Fundamental Theorem of Line Integrals - Since the closed loop has both start and end point = A, as per the theorem, $\int_{C} \nabla f \vec dr = f(A) - f(A) = 0$ In the animation below, we have $\vec F = x\hat i + y\hat j$. The line integral of any closed loop in the vector field will equal zero.
12 |
|
13 |
|
Animation 5: The line integral along a closed loop in a conservative vector field is zero |
|
And finally, another vital consequence of the fundamental theorem is discussed below - All vector fields in which the line integral between two points is path independent are gradient fields of some particular scalar function. this is another direct consequence of the theorem, elaborated in the section below. Is every vector field the gradient of some function? Vector fields are widely used in the study of several natural phenomena; the gravitational field and electrostatic field are vector fields that physicists frequently encounter. These fields have a function associated with them, called the potential function (think electric potential and gravitational potential corresponding to the examples above). If $\vec F$ with components $\vec F_{1}, \vec F_{2}$ is conservative, there exists a potential function f such that $\nabla f = \vec F$ $ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} = \vec F_{1}, \vec F_{2}$ The conservative field $\vec F$ is the gradient of the potential function f. Conversely, if a vector field is the gradient of a potential function, it is conservative. Thus words gradient field and conservative field can be used interchangeably, depending on context.
14 |
|
15 |
|
Animation 6: A conservative vector field and the potential function associated with it |
|
Example 1:
Determine whether the vector field $\vec F = x^{2}y\hat i + (y+5)\hat j$ is conservative. Solution: If $\vec F = x^{2}y\hat i + (y+5)\hat j$ is conservative, it must be path independent. In order to check whether $\vec F$ is path independent, we take two paths $C_1$ and $C_2$ which begin and terminate at the same points and compute the line integral of $\vec F$ along these paths. Consider curves $C_1$ with parametrisation $\vec r_{1} (t) = \left \langle t,t \right \rangle$, $0\leq t \leq 1$, and $C_2$ with parametrisation $\vec r_{2} (t) = \left \langle t,t^{2} \right \rangle$, $0 \leq t \leq 1$ with end points $(0,0)$ and $(1, 1)$ Then, $\int_{C_{1}} \vec F \cdot \vec dr = \int_0^1 \vec F (\vec r_1 (t)) \cdot \vec r_1 '(t) dt$ $= \int_0^1 \left \langle t^3, t + 5 \right\rangle \cdot \left \langle 1, 1 \right\rangle dt$ $= \int_0^1 (t^3 + t + 5) dt$ $= \left [ \frac{t^4}{4} + \frac{t^2}{2} + 5t\right ]_0^1$ $= \frac{23}{4}$ Similarly, $\int_{C_{2}} \vec F \cdot \vec dr = \int_0^1 \vec F (\vec r_2 (t)) \cdot \vec r_2 '(t) dt$ $= \int_0^1 \left \langle t^4, t^2 + 5 \right\rangle \cdot \left \langle 1, 2t \right\rangle dt$ $= \int_0^1 (t^4 + 2t^3 + 10t) dt$ $= \left [ \frac{t^5}{5} + \frac{t^4}{2} + 5t^2 \right ]_0^1$ $= \frac{57}{10}$ Since $\int_{C_{1}} \vec F \cdot \vec dr \neq \int_C_{2} \vec F \cdot \vec dr$, the field is not path independent, and hence not conservative. One can also use the property "the line integral along a closed curve in a conservative field is zero" to come to the same conclusion. Example 2:
Find the potential function that corresponds to the conservative vector field $\vec F = (2xy)\hat i + (x^2 + 2yz^3)\hat j + (3y^2z^2 + 2z)\hat k$ Solution: We are to find a function f such that $\nabla f = \vec F$ If $\nabla f = \vec F$, $f_x (x, y, z) = 2xy$. Integrating $f_x$ with respect to x gives $f(x, y, z) = x^2 y + g(y, z)$ for some g. Similarly, given $\nabla f = \vec F$, $x^2 + 2yz^3 = f_y (x, y, z) = x^2 + g_y (y,z)$ Therefore, $g_y (y,z) = 2yz^3$ Which upon integration with respect to y gives $g = y^2 z^3 + h(z)$ for some h. Hence, the function f can be written as $f(x,y,z) = x^2 y + g( y, z) = x^2 y + y^2 z^3 + h(z)$ Now we are left with the task of finding h in order to determine f. Since f is a potential function, $3y^2z^2 + 2z = g_z(y,z) = 3y^2z^2 + h'(z)$ which implies that $h'(z = 2z)$, and consequently that $h(z) = z^2 + C$. Therefore, for $C = 0$, the potential function f is $f(x,y,z) = x^2 y + g( y, z) = x^2 y + y^2 z^3 + z^2$ This can be verified by substituting these values into the equation $\nabla f = \vec F$ ApplicationsVector fields are studied in various sub-domains of the physical sciences. In mechanics, the gravitational field, in electromagnetism, the electric and magnetic fields, and in fluid mechanics, the velocity field - knowledge of whether the field is conservative or not has important implications. Non-conservative fields have equally significant consequences. Perpetual Motion MachinesAs its name suggests, a perpetual motion machine moves perpetually, without losing energy. If such a machine existed, it would be able to produce energy out of nothing. The law of conservation of energy, the laws of thermodynamics, the anthropic principle could all be used to justify the impossibility of this machine. Conservative fields make the construction of such machines an impossibility. Take for example the gravitational field, which, due to its energy preserving nature, does not allow more energy to be produced than consumed in the operation of the machine.
16 |
|
17 |
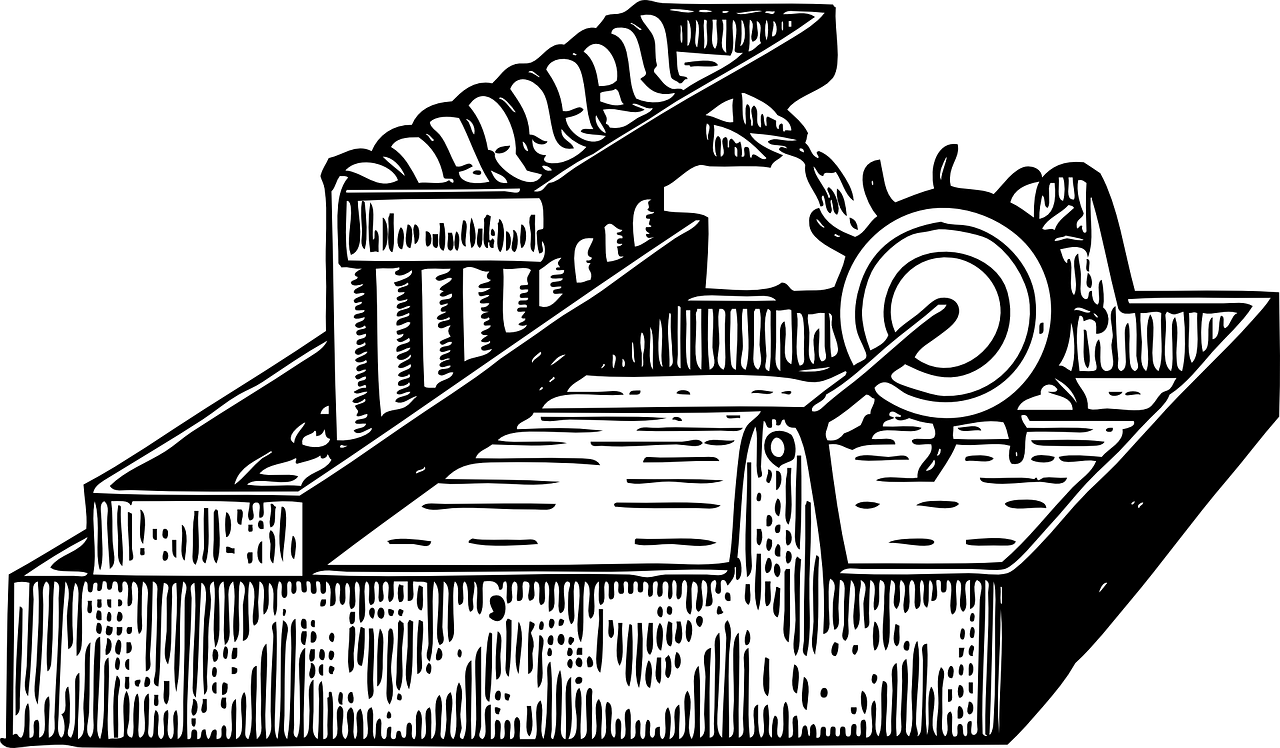
Figure 2: A perpetual motion machine |
HistoryThe study of conservative fields and their corresponding conservative force fields was, as it continues to be, an integral part of physics. As vector calculus developed, conservative fields evolved into what mathematicians and physicists considered one of the foremost implications of the Fundamental Theorem of Line Integrals. Since time immemorial, mankind has been pursuing the construction of perpetual motion machines. Back in the middle ages, it was not known whether or not such machines were possible to construct. Today, although there is no formal proof of its impossibility, the study of conservative fields in vector calculus assures engineers that any attempt to construct such a machine would end in vain. Nevertheless, there are people still trying to harness the power of modern science and technology to achieve this impossible task.
Apart from the physical sciences and engineering, conservative fields find their applications in other, seemingly unrelated areas too. Take art, for example. The figures below are lithograph prints by the Dutch artist M.C Escher. They capture perfectly the idea of conservative fields. 18 |
|
19 |

Figure 2: Waterfall, by M.C Escher, first printed in October 1961 |
Pause and Ponder
Why is it that when an apple falls from a height under the influence of gravity, it doesn't spin?(Ignore effects of air resistance, wind, weather, external disturbances) Hint: Think about rotation and the operator in vector calculus that is associated with it. 20 |
|
21 |

Figure 4: Isaac Newton's famous apple tree |
Hint: Recall from the lecture on the gradient operator that level curves of a gradient field do not intersect. 22 |
|
23 |
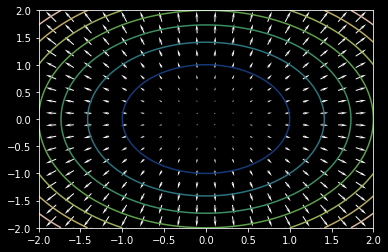
Figure 5: Vector field 1 |
|
24 |
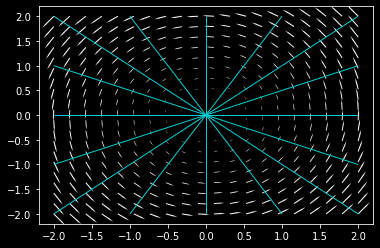
Figure 6: Vector field 2 |
Note: Although the Laplacian is not introduced in these notes, it is mentioned here for the sake of completeness 1. Divergence of curl is 0
$\nabla \cdot (\nabla \times \vec F) = 0$ 2. Divergence of divergence is undefined $\nabla \cdot (\nabla \cdot \vec F) = \textrm{undefined}$ 3. Divergence of gradient is laplacian $\nabla \cdot (\nabla f) = \nabla^2 f$ 4. Curl of curl is the vector laplacian $\nabla \times (\nabla \times \vec F) = \nabla (\nabla \cdot A) - \nabla^2 A$ 5. Curl of divergence is undefined $\nabla \cdot (\nabla \times \vec F) = 0$ 6. Curl of gradient is 0 $\nabla \times (\nabla f) = 0$ 25 |
Further Reading
References
26 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
