Tangent Plane Approximations |
|---|
DefinitionSuppose $z = f(x,y)$ is a function having continuous first-order partial derivatives and the equation of tangent plane is given as $$ z – z_0 = f_x (x_0 , y_0 )(x – x_0 ) + f_y (x_0 , y_0 )(y – y_0 )$$ at the point $(x_0,y_0)$ on $f$. Then $\begin{equation}\label{eq:tpa}z \approx z_0 + f_x (x_0 , y_0 )(x – x_0 ) + f_y (x_0 , y_0 )(y – y_0 ) \tag{1}\end{equation}$ is called the tangent plane approximation of $f$ for point $(x,y)$ lying near to the point $(x_0,y_0)$ on the surface of the function.
0 |
|
0 |
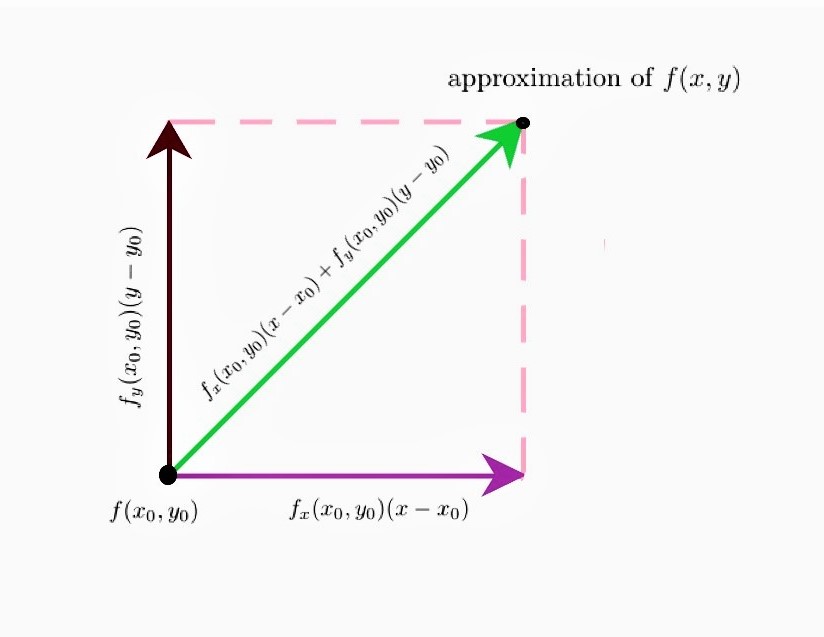
Figure 1: Tangent Plane Approximation |
MotivationIn the real world there is often, not an equation, just data that describes a system, and approximation is one of the best ways that one can use to handle such numerical data. For example, the weather department collects data of windchill (Windchill is a term used to describe what the air temperature feels like to the human skin due to the combination of cold temperatures and winds blowing on exposed skin) depending on the velocity of the wind and temperature, ie, windchill is a function of wind velocity and temperature. $$w=f(v, T)$$ The tangent plane approximation can be used to predict the windchill $w$ at some point $(v,T)$ which lies near to the point $(v_0, T_0)$, where the known quantities would be: values $(v,T)$ and $(v_0,T_0)$, $w_0$ (value of $w$ at $(v_0,T_0)$) and the unknown quantity would be: the value of $w$ at $(v,T)$ The approximation of the equation of the tangent plane would be: $$w \approx w_0+f_v(v_0,T_0)(v-v_0)+f_T(v_0,T_0)(T-T_0)$$ Thus the windchill ($w$) at $(v,T)$ can be determined using the above equation. Therefore, the tangent plane approximation provides a way to approximate the value of a function, to a certian degree of accuracy, for some random point with the help of a given set of data or information, and it also helps to determine how a function changes w.r.t to the changes in its input variables. 0 |
Bird's Eye ViewConsider a smooth surface described by a differentiable function $f$ and consider some point $(x,y)$ on the surface. Looking closely at and around that point, the surface would appear to look like a plane.What this means is that, we can study the function around that point by replacing the surface with a plane that touches the the surace only at $(x,y)$. This plane is called the tangent plane. This tangent plane is used to approximate the values of the function at the points that lie near $(x,y)$, on the surface, described by the function.
0 |
|
0 |
|
Video 1 : Tangent Plane |
Context of DefinitionAccording to the equation ($\ref{eq:tpa}$) in the definition, $ z_0$ is the value of $f$ at the point $(x_0,y_0)$ (1.a) $f_x(x_0,y_0)$ is the rate of change of $f$ at $(x_0,y_0)$ in $x$ direction $f_y(x_0,y_0)$ is the rate of change of $f$ at $(x_0,y_0)$ in $y$ direction $(x-x_0)$ is the distance moved from $x_0$ in $x$ direction $(y-y_0)$ is the distance moved from $y_0$ in $y$ direction For a function of two variables $f(x,y)$, suppose the first partial derivatives of $f$, $f_x$ and $f_y$, exist at $(x_0,y_0)$. A plane that best approximates $f(x,y)$ near $(x_0,y_0)$ must pass through the point $(x_0,y_0,z_0)$, and the slope of the plane in the $x$ and $y$ directions should be equal to the values of $f_x(x_0,y_0)$ and $f_y(x_0,y_0)$ respectively.
Derivation:Since a general linear function $L$ of two variables $x$ and $y$ can be written as $L = f(x,y)$ and is described by the formula $$\begin{equation}\label{eq:leq} L=A(x-x_0)+B(y-y_0)+C \tag{2}\end{equation}$$ where $C$ is a linear function in $(x_0,y_0)$ ie, $C = f(x_0,y_0)$ and $$A=\frac{\partial L_{(x_0,y_0)}}{\partial x} $$ $$B=\frac{\partial L_{(x_0,y_0)}}{\partial y} $$ Substituting values of $A,B,C$ in ($\ref{eq:leq}$) gives another linear function that best approximates $f(x,y)$ near $(x_0,y_0)$ ie, the tangent plane approximation $$L= C+ \frac{\partial L_{(x_0,y_0)}}{\partial x}(x-x_0)+ \frac{\partial L_{(x_0,y_0)}}{\partial y}(y-y_0)$$ $$\implies f(x,y) = f(x_0,y_0)+ f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$$ $$\implies z = z_0+ f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$$ $z=f(x,y)$ (from the definition) and $z_0 = f(x_0,y_0)$ (from 1.a)
0 |
|
The idea behind using the tangent plane approximation is that there is a point $(x_0,y_0)$ on the surface of the function at which the precise value of the function $f$ is known, then for all the values of $(x,y)$ lying in the nearby neighborhood of $(x_0,y_0)$, the tangent plane approximation yields a value that is also reasonably close to the exact value of $f(x_0,y_0)$. The following animation visualizes the tangent plane approximation as drawn in Figure 1. 0 |
|
0 |
|
Video 2: Tangent plane approximation visualization |
Tangent PlaneIn three-dimensional space, many lines can be tangent to a given point. The plane containing all these tangent lines determines the tangent plane at that point. Thus, a tangent plane at a particular point on the surface of the function contains all of the lines tangent to that point and is parallel to the surface at that point. For a specific point on the surface of the function, only one (unique) tangent plane exists parallel to the surface at that point. Derivation of the tangent plane equation:Let $(x_0,y_0,z_0)$ be a point on the surface of the function $z = f(x,y)$ where $f$ is differentiable at $(x_0,y_0)$. The equation of the plane passing through $(x_0,y_0,z_0)$ has the form $$\begin{equation}\label{eq:tpe}A(x-x_0)+B(y-y_0)+C(z-z_0)=0\tag{3}\end{equation}$$ Dividing eq.(\ref{eq:tpe}) by $C$: $$\begin{equation}\label{eq:tpl}a(x-x_0)+b(y-y_0)-(z-z_0)=0\tag{3.a}\end{equation}$$ where $a = -\frac{A}{C}$ and $b = -\frac{B}{C}$ Now, taking $y$ constant $(y=y_0)$ in eq.(\ref{eq:tpl}) will give: $$(z-z_0) = a(x-x_0)$$ This is the equation of the line passing through point $(x,y_0)$ and its is the of the form $y = mx$ (equation of a line). Therefore, $a$ is the slope of the tangent line to the surface at the point $(x,y_0)$. This slope is the partial derivative of $f$ with respect to $x$ at $(x_0,y_0)$. Hence, $a=f_x(x_0,y_0)$. Similarly, holding $x$ constant $(x=x_0)$, gives $b=f_y(x_0,y_0)$ ($b$ will be the slope of the tangent line to the surface at the point $(x_0,y)$). Substituting values of $a$ and $b$ in eq.(\ref{eq:tpl}): $$ f_x (x_0 , y_0 )(x – x_0 ) + f_y (x_0 , y_0 )(y – y_0 ) - (z – z_0)=0$$ $$\begin{equation}\label{eq:pla}\implies (z – z_0)= f_x (x_0 , y_0 )(x – x_0 ) + f_y (x_0 , y_0 )(y – y_0 )\tag{3.b}\end{equation}$$ The eq.(\ref{eq:pla}) is the equation of the tangent plane to the surface of $z=f(x,y)$ at the point $(x_0,y_0,z_0)$.
The tangent plane will not exist for $f$ if it is not differentiable at any point $(x_0,y_0)$ because zooming in on the point does not show a plane surface. This case is demonstrated by the following animation.
0 |
|
0 |
|
Video 3: Non Differentiable Function |
|
Tangent Plane for all the extrema and saddle points of a function is always parallel to the $x$-$y$ plane and it is also parallel to the surface of the function at the extrema and saddle point. The following animation visualizes the existence of the tangent plane at extrema and saddle points. 0 |
|
0 |
|
Video 4: Tangent plane at extrema and Saddle Point |
Applications
0 |
HistoryThe problem of finding the tangent to a curve has been studied by many mathematicians since Archimedes explored the question in Antiquity. The first attempt at determining the tangent to a curve that resembled the modern method of the Calculus came from Gilles Persone de Roberval between 1630-40. In his book Traité des Indivisibles (dated 1634), Roberval generalized a method Archimedes had used to find the tangent at any point in his spiral. Like Archimedes, Roberval thought of a curve as the locus of a point moving under the action of two velocities. Pierre de Fermat used the notion of maxima and the infinitesimal to find the tangent to a curve. His method for finding a tangent was developed during the 1630s, it was almost exactly the method used by Newton and Leibniz although it lacked the formal concept of a limit. 0 |
Pause and Ponder
1 |
References$[1]$ http://faculty.up.edu/wootton/Calc3/Section15.4.pdf $[2]$ https://www.foi.se/rest-api/report/FOI-R--0988--SEhttps://www.foi.se/rest-api/report/FOI-R--0988--SE $[3]$ https://www.math.usm.edu/math/lambers/mat280/spr10/lecture5.pdf $[4]$ https://ocw.aprende.org/resources/res-18-001-calculus-online-textbook-spring-2005/textbook/MITRES_18_001_strang_13.pdf 1 |
Further Reading
1 |
| Contributor: |
| Mentor & Editor: |
| Verified by: |
| Approved On: |
The following notes and their corrosponding animations were created by the above-mentioned contributor and are freely avilable under CC (by SA) licence. The source code for the said animations is avilable on GitHub and is licenced under the MIT licence.
